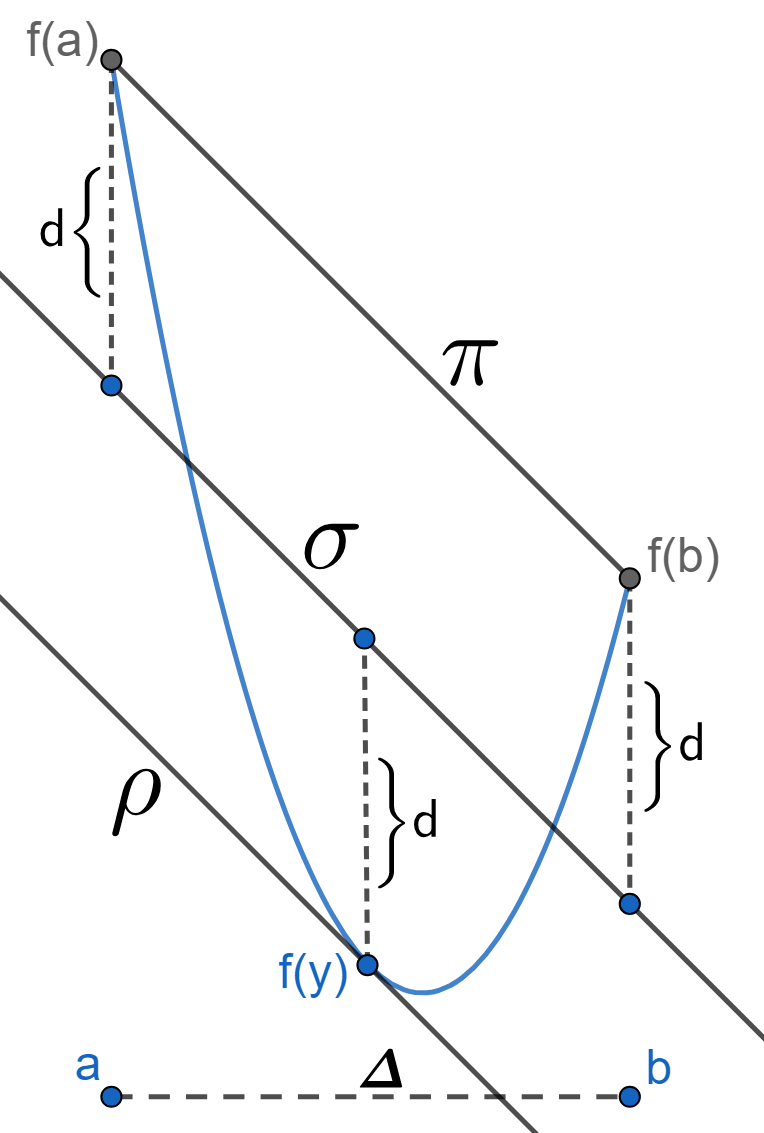
We study Min-Max affine approximants of a continuous convex or concave function $f:\Delta\subset \mathbb R^k\xrightarrow{} \mathbb R$ where $\Delta$ is a convex compact subset of $\mathbb R^k$. In the case when $\Delta$ is a simplex we prove that there is a vertical translate of the supporting hyperplane in $\mathbb R^{k+1}$ of the graph of $f$ at the vertices which is the unique best affine approximant to $f$ on $\Delta$. For $k=1$, this result provides an extension of the Chebyshev equioscillation theorem for linear approximants. Our result has interesting connections to the computer graphics problem of rapid rendering of projective transformations.
翻译:我们研究的是连续 convex 函数或 concave 函数的 Min- Max 的 Min- Max affin 近似值 $f:\ Delta\ subset\ mathbb Räk\xrightrow\\\ mathbR \\ mathbR$\ delta$\ delta$ 是 mathbRik\ xrightrowr\\\ mathbrookR$ 的 convax 。 当 $\ delta$ 是 mathbrb Räk+1} 时, 我们证明在 $\ mathb Rák+1} 的顶端点上的 $f( $f) 的支持性超高平面有一个垂直翻译 。 顶点是 $\\\ mathb Rák+1} $ ( $ folf) 。 这是独一无二的顶点 顶点 aprox- fon the polf at the polf sublex polex suction suction suction sub sub the sub suffect of the suffect of the subly sublections sublections subly.