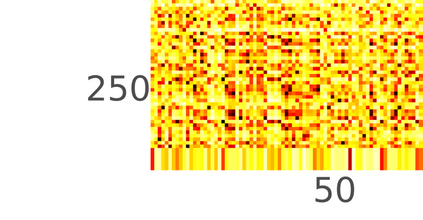
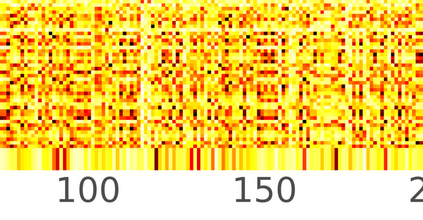
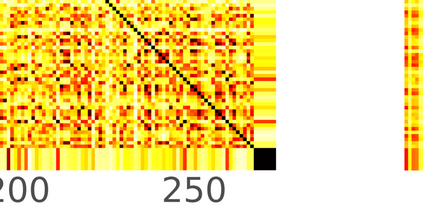
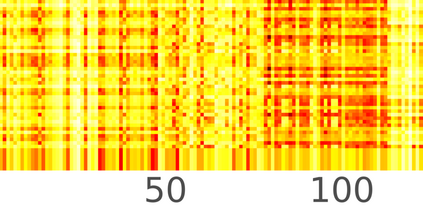
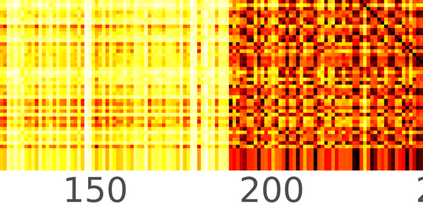
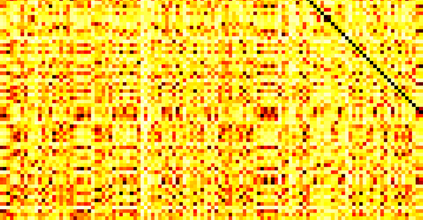
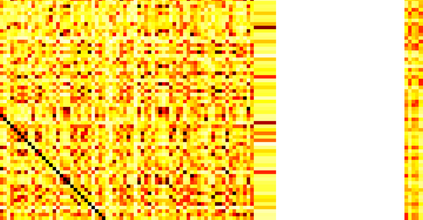
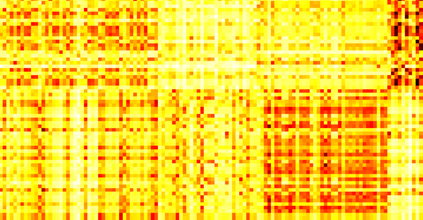
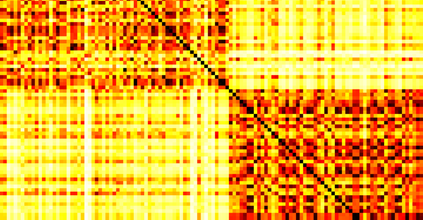
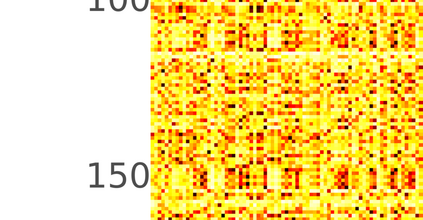
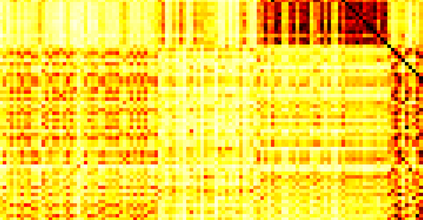
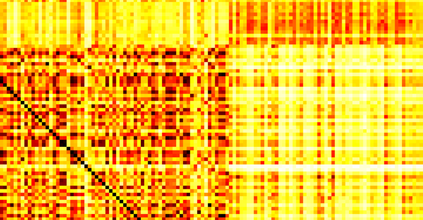
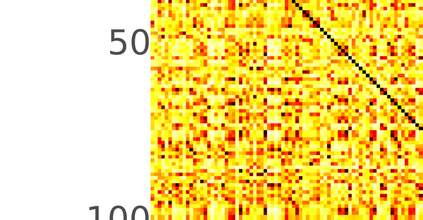
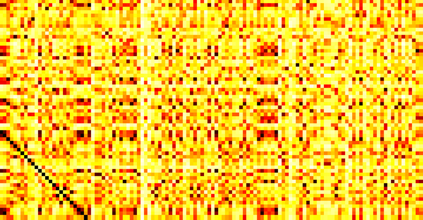
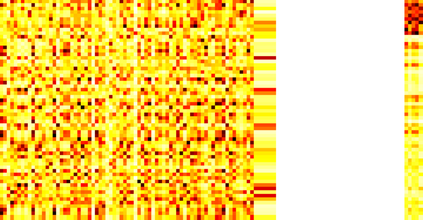
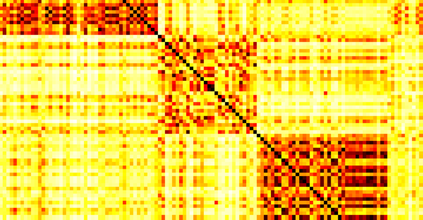
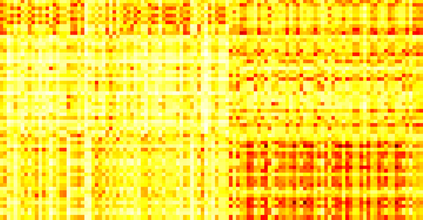
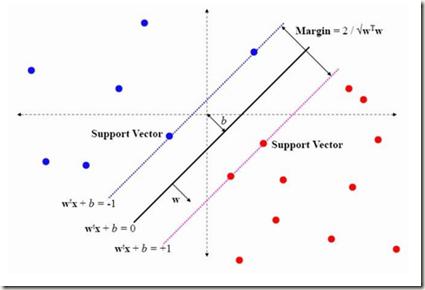
Typically, nonlinear Support Vector Machines (SVMs) produce significantly higher classification quality when compared to linear ones but, at the same time, their computational complexity is prohibitive for large-scale datasets: this drawback is essentially related to the necessity to store and manipulate large, dense and unstructured kernel matrices. Despite the fact that at the core of training a SVM there is a \textit{simple} convex optimization problem, the presence of kernel matrices is responsible for dramatic performance reduction, making SVMs unworkably slow for large problems. Aiming to an efficient solution of large-scale nonlinear SVM problems, we propose the use of the \textit{Alternating Direction Method of Multipliers} coupled with \textit{Hierarchically Semi-Separable} (HSS) kernel approximations. As shown in this work, the detailed analysis of the interaction among their algorithmic components unveils a particularly efficient framework and indeed, the presented experimental results demonstrate a significant speed-up when compared to the \textit{state-of-the-art} nonlinear SVM libraries (without significantly affecting the classification accuracy).
翻译:一般来说,非线性支持矢量机(SVM)的分类质量比线性矢量机(SVM)的分类质量要高得多,但与此同时,它们的计算复杂性对大规模非线性SVM问题来说却令人望而却步:这一缺陷基本上与储存和操作大型、密集和无结构的内核矩阵的必要性有关。尽管在SVM培训的核心存在一个\textit{speal} convex优化问题,但内核质的存在导致性能急剧下降,使SVMS无法工作地缓慢应对大问题。为了有效解决大规模非线性SVM问题,我们提议使用“Textit{alting 方向方法” 与\textit{HSS) 高层次半可分离内核近近。如这项工作所示,对其算法组成部分之间相互作用的详细分析揭示了一个特别有效的框架,而且事实上,提出的实验结果表明,与显著地影响数据级/Mart非图书馆(Star-Star) 对比,速度非常快。