Average causal effect estimation via instrumental variables: the no simultaneous heterogeneity assumption

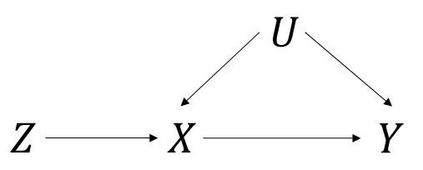
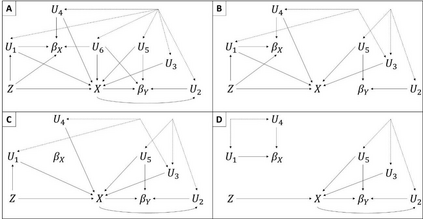
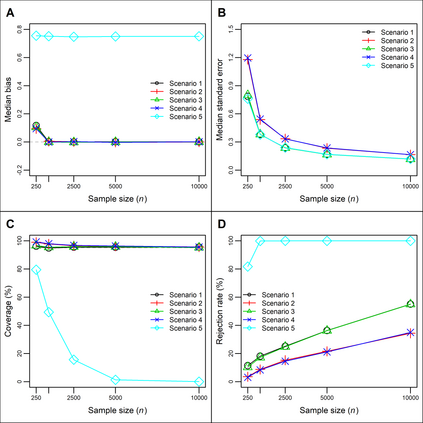
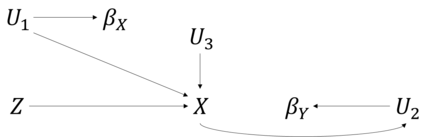
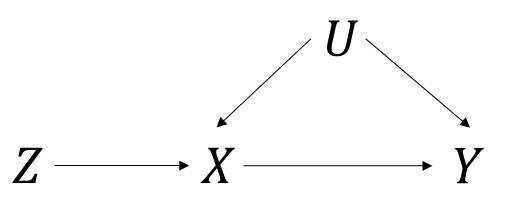
Instrumental variables (IVs) can be used to provide evidence as to whether a treatment X has a causal effect on Y. Z is a valid instrument if it satisfies the three core IV assumptions of relevance, independence and the exclusion restriction. Even if the instrument satisfies these assumptions, further assumptions are required to estimate the average causal effect (ACE) of X on Y. Sufficient assumptions for this include: homogeneity in the causal effect of X on Y; homogeneity in the association of Z with X; and No Effect Modification (NEM). Here, we describe the NO Simultaneous Heterogeneity (NOSH) assumption, which requires the heterogeneity in the Z-X association and heterogeneity in the X-Y causal effect to be independent. We describe the necessary conditions for NOSH to hold, in which case conventional IV methods are consistent for the ACE even if both homogeneity assumptions and NEM are violated. We illustrate these ideas using simulations and by re-examining selected published studies.