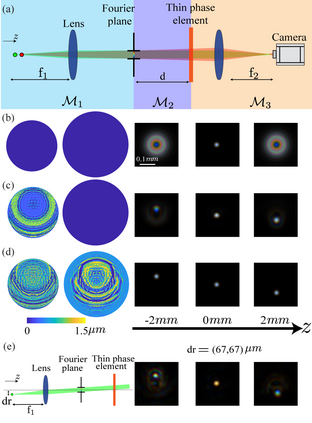
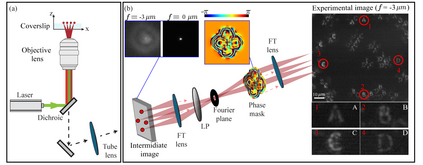
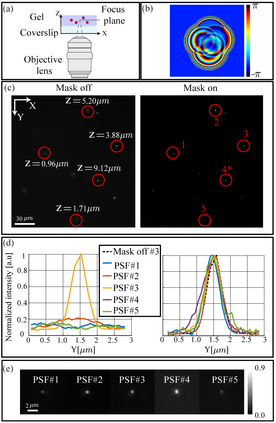
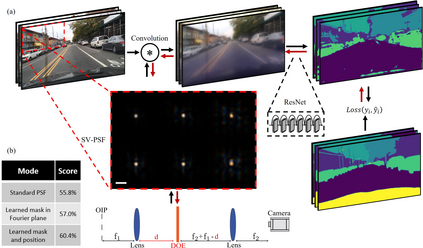
Modern design of complex optical systems relies heavily on computational tools. These typically utilize geometrical optics as well as Fourier optics, which enables the use of diffractive elements to manipulate light with features on the scale of a wavelength. Fourier optics is typically used for designing thin elements, placed in the system's aperture, generating a shift-invariant Point Spread Function (PSF). A major bottleneck in applying Fourier Optics in many cases of interest, e.g. when dealing with multiple, or out-of-aperture elements, comes from numerical complexity. In this work, we propose and implement an efficient and differentiable propagation model based on the Collins integral, which enables the optimization of diffraction optical systems with unprecedented design freedom using backpropagation. We demonstrate the applicability of our method, numerically and experimentally, by engineering shift-variant PSFs via thin plate elements placed in arbitrary planes inside complex imaging systems, performing cascaded optimization of multiple planes, and designing optimal machine-vision systems by deep learning.
翻译:复杂的光学系统现代设计严重依赖计算工具。这些系统通常使用几何光学和Fourier光学,能够使用不同功能来利用波长尺度的光来操纵光线。 Fourier光学通常用于设计稀薄元素,放在系统的孔径中,产生一个变换点扩展功能(PSF),在许多有兴趣的情况下应用Fourier光学存在一个重大瓶颈,例如,处理多重或外孔元素时,来自数字复杂性。在这项工作中,我们提议并采用基于Collins 集成的高效和不同的传播模型,以便利用反向再造法优化具有前所未有的设计自由的折叠式光学系统。我们通过在复杂成像系统中任意飞机上放置的薄质板元素,从数字上和实验上展示了我们的方法的适用性,我们的方法是:通过在复杂的成像系统中的任意式成型式成型的变压式 PSFSFSF,对多架飞机进行级优化,并通过深学设计最佳的机器造型系统。