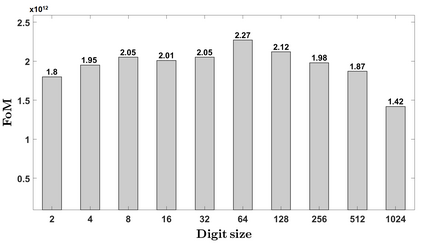
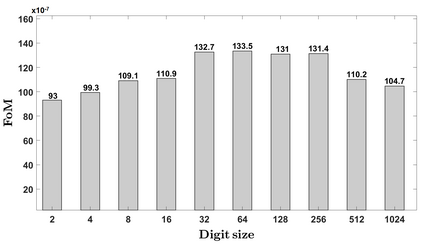
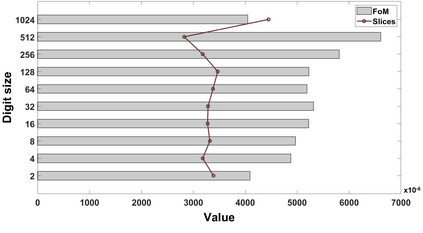
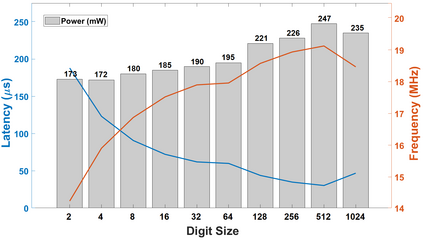
Polynomial multiplication is a bottleneck in most of the public-key cryptography protocols, including Elliptic-curve cryptography and several of the post-quantum cryptography algorithms presently being studied. In this paper, we present a library of various large integer polynomial multipliers to be used in hardware cryptocores. Our library contains both digitized and non-digitized multiplier flavours for circuit designers to choose from. The library is supported by a C++ generator that automatically produces the multipliers' logic in Verilog HDL that is amenable for FPGA and ASIC designs. Moreover, for ASICs, it also generates configurable and parameterizable synthesis scripts. The features of the generator allow for a quick generation and assessment of several architectures at the same time, thus allowing a designer to easily explore the (complex) optimization search space of polynomial multiplication.
翻译:多元乘法是大多数公用钥匙加密协议中的一个瓶颈,包括正在研究的 Elliptic-curve 密码学和数子系后加密算法。在本文中,我们展示了用于硬件加密核的各种大整数多元乘数的图书馆。我们的图书馆包含供电路设计师选择的数字化和非数字化乘数调味料。图书馆得到一个C++生成器的支持,该生成器自动生成Verilog HDL中的乘数逻辑,供FPGA和ACICE设计使用。此外,对于ASICs来说,它还生成可配置和可参数合成的合成脚本。生成器的特性允许快速生成并同时评估若干结构,从而使设计师能够方便地探索多相乘的(复合)优化搜索空间。