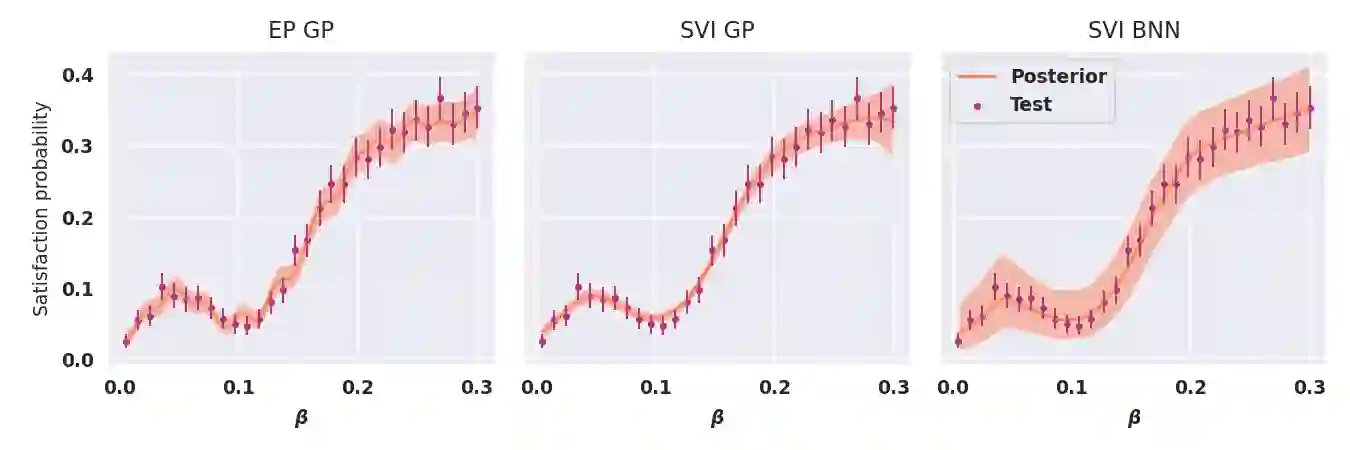
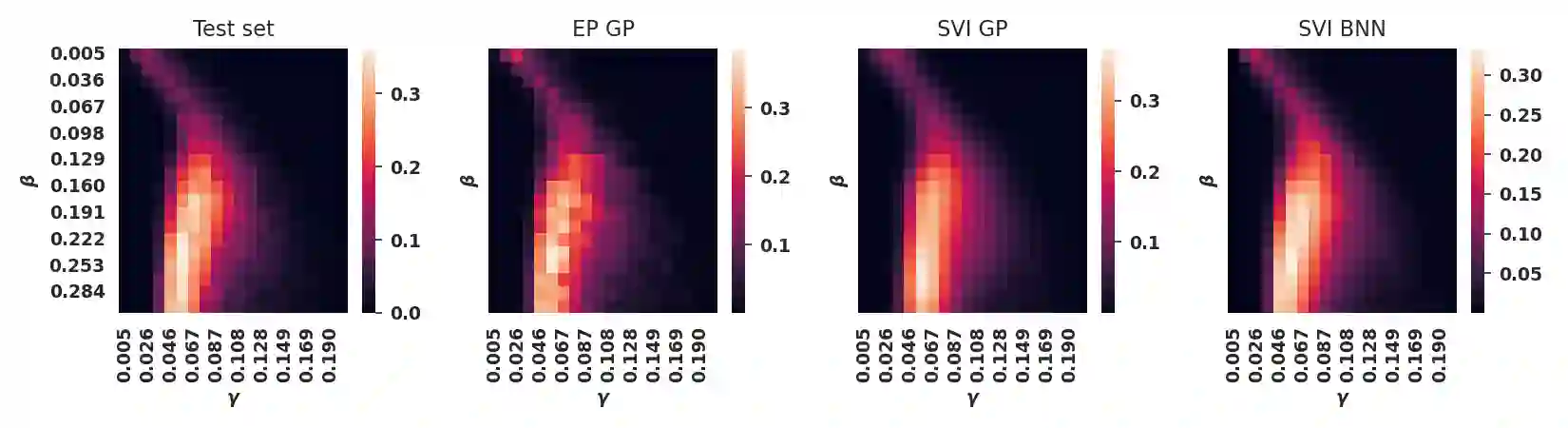
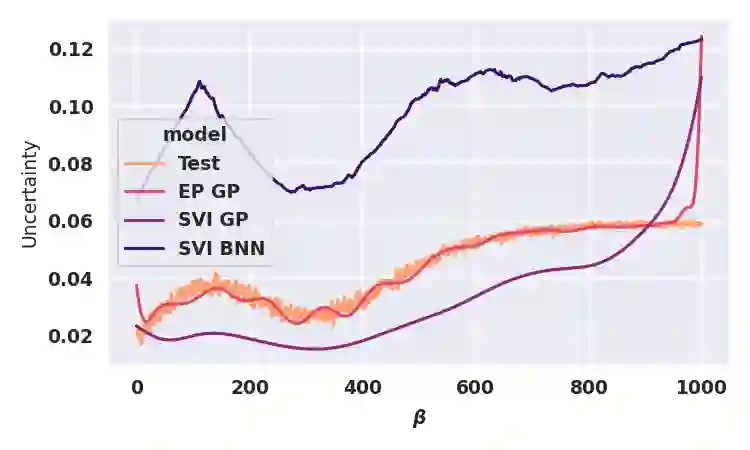
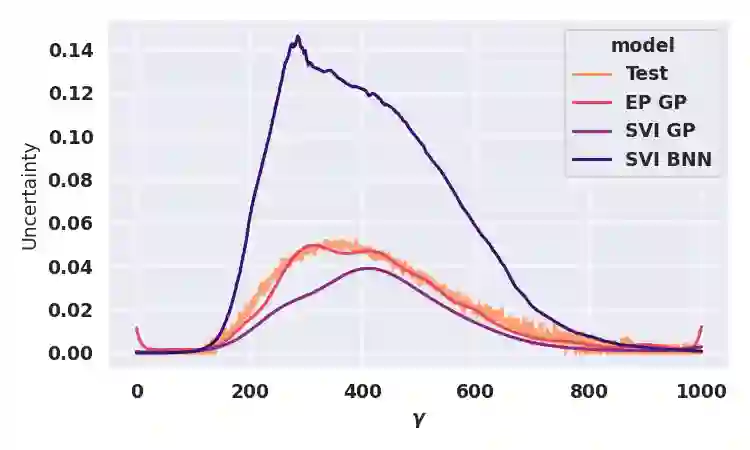
Model-checking for parametric stochastic models can be expressed as checking the satisfaction probability of a certain property as a function of the parameters of the model. Smoothed model checking (smMC) leverages Gaussian Processes (GP) to infer the satisfaction function over the entire parameter space from a limited set of observations obtained via simulation. This approach provides accurate reconstructions with statistically sound quantification of the uncertainty. However, it inherits the scalability issues of GP. In this paper, we exploit recent advances in probabilistic machine learning to push this limitation forward, making Bayesian inference of smMC scalable to larger datasets, enabling its application to larger models in terms of the dimension of the parameter set. We propose Stochastic Variational Smoothed Model Checking (SV-smMC), a solution that exploits stochastic variational inference (SVI) to approximate the posterior distribution of the smMC problem. The strength and flexibility of SVI make SV-smMC applicable to two alternative probabilistic models: Gaussian Processes (GP) and Bayesian Neural Networks (BNN). Moreover, SVI makes inference easily parallelizable and it enables GPU acceleration. In this paper, we compare the performances of smMC against those of SV-smMC by looking at the scalability, the computational efficiency and at the accuracy of the reconstructed satisfaction function.
翻译:模型校验模拟模型可以表现为检查某种属性的满意度概率,作为模型参数的函数。平滑的模型检查(SmMC)将Gausian Processes(GP)从通过模拟获得的一组有限的观测中推导出整个参数空间的满意度功能。这个方法提供了精确的重建,对不确定性进行了统计上合理的量化。但它继承了GP的可缩放问题。在本文中,我们利用了最近在概率机器学习方面的进步来推动这一限制,使BayesaMC的缩放推向更大的数据集,使其在参数集的维度尺寸方面适用于更大的模型。我们建议了Stochati Variation 模型检查(SV-smMC),这一解决方案利用了随机变异性推法(SVI)来估计SmMC问题的后表分布。SVI的强度和灵活性使SV-mMC的SmMC适用于两种替代性的可比较性能模型:Gals-vicality,使GMIS的Servial Syal Provial (Gs) 和Syal SIal SIal 的Scial 和Syal IMal 的Syal 。使GIL 和SILILA) 和SGILA 和SILI 的快速的快速的SI II 。