Coefficients' Settings in Particle Swarm Optimization: Insight and Guidelines

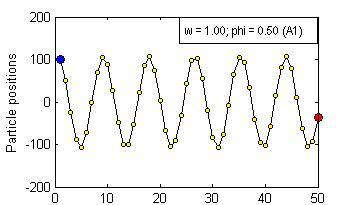
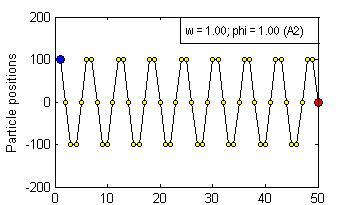
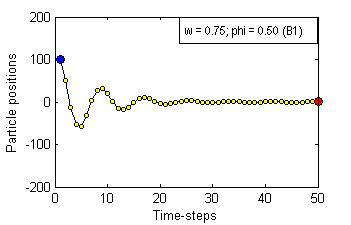
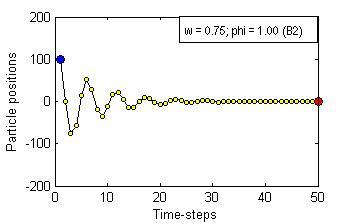
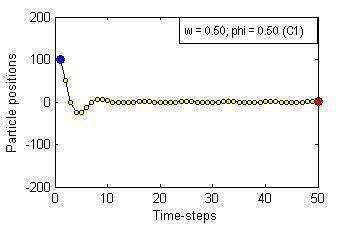
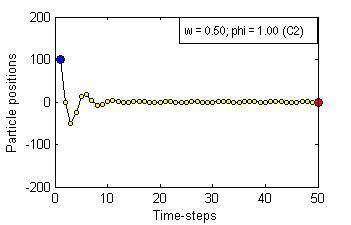
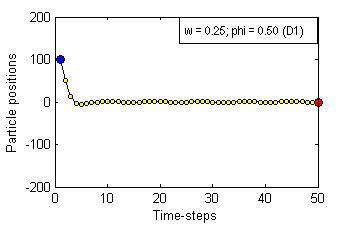
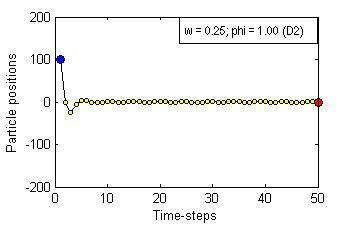
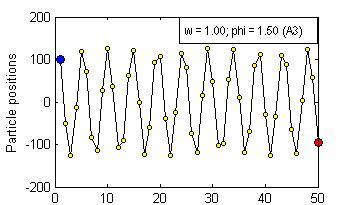
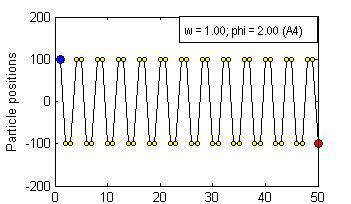
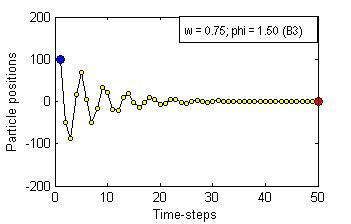
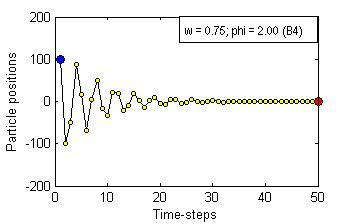
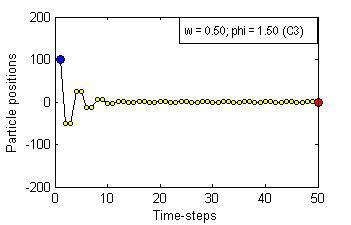
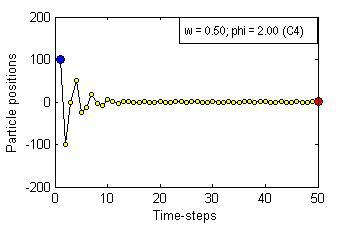
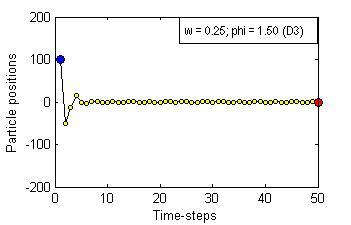
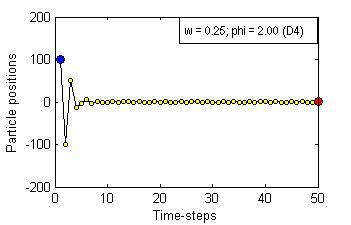
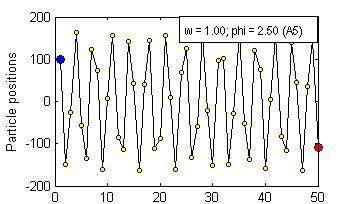
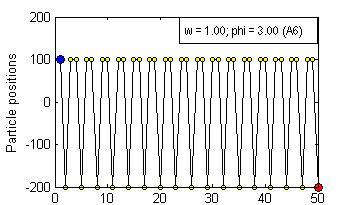
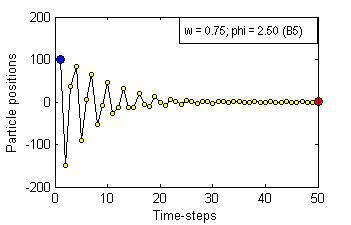
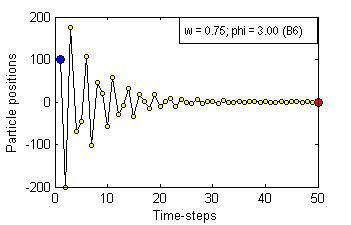
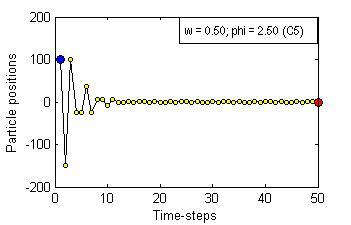
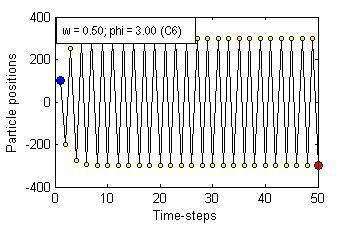
Particle Swam Optimization is a population-based and gradient-free optimization method developed by mimicking social behaviour observed in nature. Its ability to optimize is not specifically implemented but emerges in the global level from local interactions. In its canonical version, there are three factors that govern a particle's trajectory: 1) inertia from its previous displacement; 2) attraction to its best experience; and 3) attraction to a given neighbour's best experience. The importance given to each of these factors is regulated by three coefficients: 1) the inertia; 2) the individuality; and 3) the sociality weights. Their settings rule the trajectory of the particle when pulled by these two attractors. Different speeds and forms of convergence of a particle towards its attractor(s) take place for different settings of the coefficients. A more general formulation is presented aiming for a better control of the embedded randomness. Guidelines to select the coefficients' settings to obtain the desired behaviour are offered. The convergence speed of the algorithm also depends on the speed of spread of information within the swarm. The latter is governed by the structure of the neighbourhood, whose study is beyond the scope of this paper. The objective here is to help understand the core of the PSO paradigm from the bottom up by offering some insight into the form of the particles' trajectories, and to provide some guidelines as to how to decide upon the settings of the coefficients in the particles' velocity update equation in the proposed formulation to obtain the type of behaviour desired for the problem at hand. General-purpose settings are also suggested. The relationship between the proposed formulation and both the classical and constricted PSO formulations are also provided.