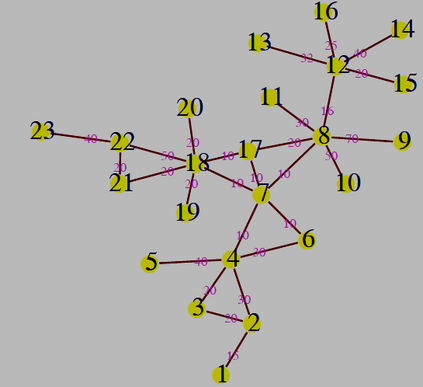
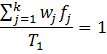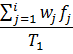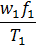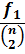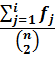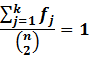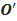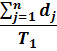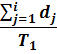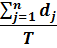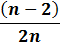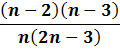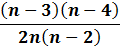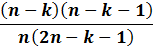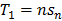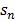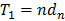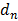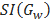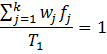A majority of real life networks are weighted and sparse. The present article aims at characterization of weighted networks based on sparsity, as a measure of inherent diversity, of different network parameters. It utilizes sparsity index defined on ordered degree sequence of simple networks and derives further properties of this index. The range of possible values of sparsity index of any connected network, with edge-count in specific intervals, is worked out analytically in terms of node-count; a pattern is uncovered in corresponding degree sequences to produce highest sparsities. Given the edge-weight frequency distribution of a network, we have formulated an expression of the sparsity index of edge-weights. Its properties are analyzed under different distributions of edge-weights. For example, the upper and lower bounds of sparsity index of edge-weights of a network, having all distinct edge-weights, is determined in terms of its node-count and edge density. The article highlights that this summary index with low computational cost, computed on different network parameters, is useful to reveal different structural and organizational aspects of networks for performing analysis. An application of this index has been demonstrated through overlapping community detection of networks. The results validated on artificial and real-world networks show its efficacy.
翻译:多数实际生命网络是加权和稀疏的。本条款旨在根据宽度对基于宽度的加权网络进行定性,以衡量不同网络参数的内在多样性。它使用按简单网络的顺序顺序顺序排列的宽度指数,并得出该指数的进一步特性。任何联网网络的宽度指数的可能值范围,以特定的间距计算边缘值,从节点计的角度进行分析性地确定;在产生最大宽度的相应程度序列中发现一种模式。鉴于网络的边重频率分布,我们制定了边缘重量的宽度指数的表达方式。在边缘重量的不同分布下分析其特性。例如,一个网络的边重的宽度指数的上下界限,以所有不同的边重计算和边宽度密度来决定。文章强调,根据不同的网络参数计算,这一计算成本低的汇总指数有助于揭示网络的不同结构和组织方面。这一指数的特性在边缘重量的不同分布下分析。其特性在边缘重量分布的不同分布下得到分析。例如,一个网络的边重度指数的上下边缘指数的宽度指数,以其所有不同的边重的边重和边宽密度为确定。文章强调,根据不同的网络参数计算成本计算成本计算,有助于揭示出网络的不同结构和和组织方面。该指数的应用。该指数的应用已经通过对网络加以验证,从而显示其实际效率网络的网络的网络的相互校验。