Random and quasi-random designs in group testing

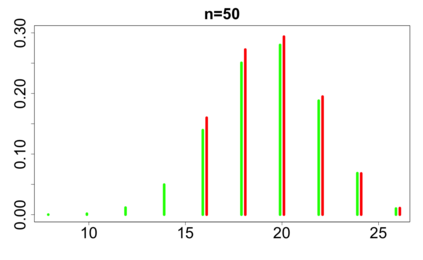
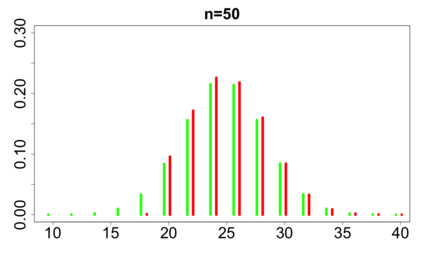
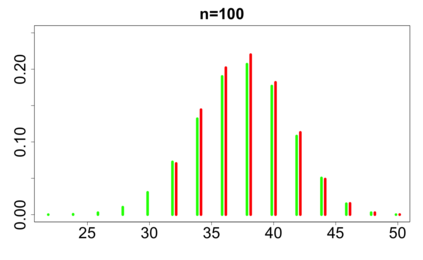
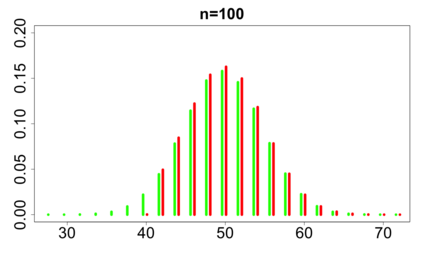
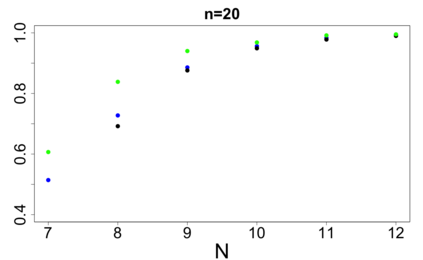
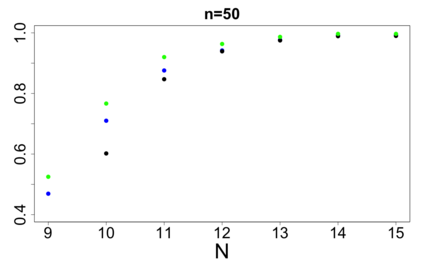
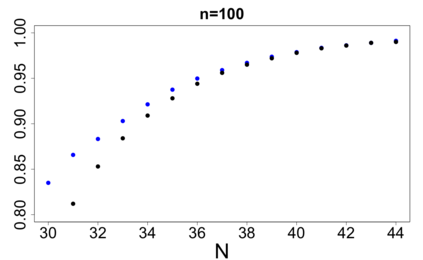
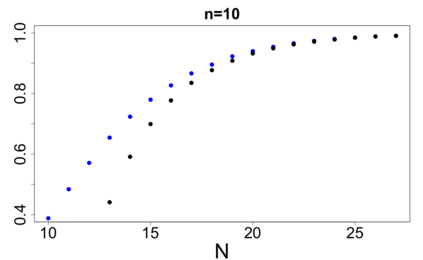
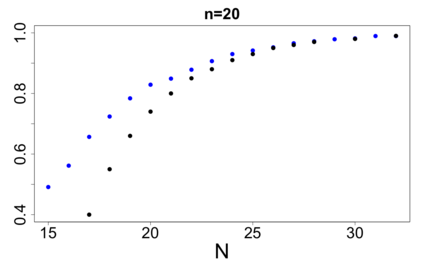
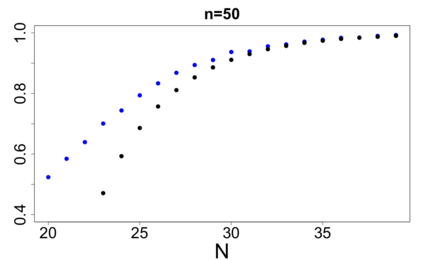
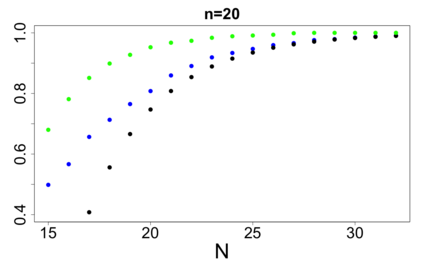
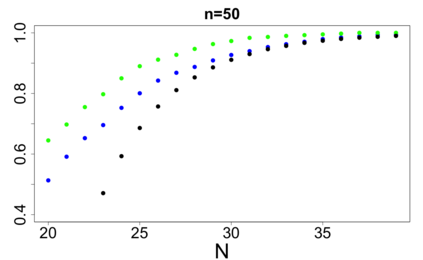
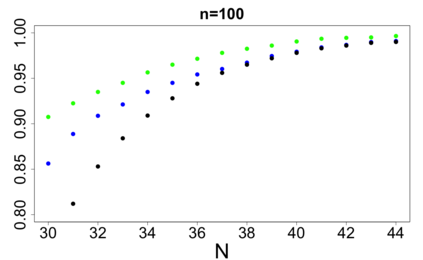
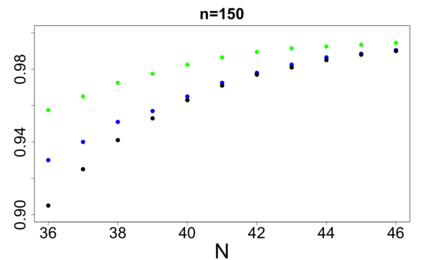
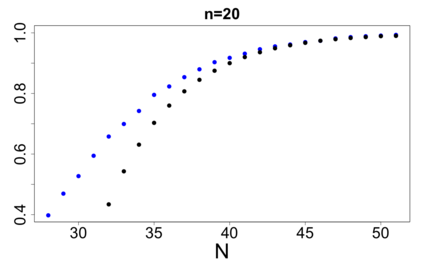
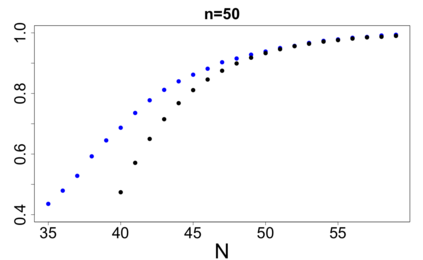
For large classes of group testing problems, we derive lower bounds for the probability that all significant factors are uniquely identified using specially constructed random designs. These bounds allow us to optimize parameters of the randomization schemes. We also suggest and numerically justify a procedure of construction of designs with better separability properties than pure random designs. We illustrate theoretical consideration with large simulation-based study. This study indicates, in particular, that in the case of the common binary group testing, the suggested families of designs have better separability than the popular designs constructed from the disjunct matrices.