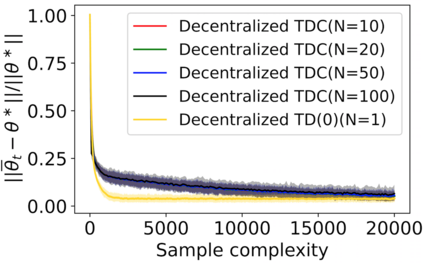
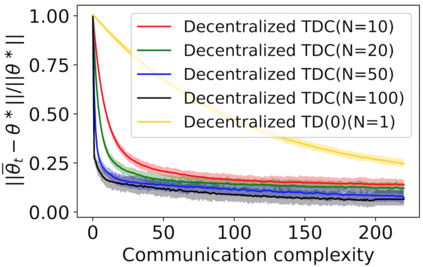
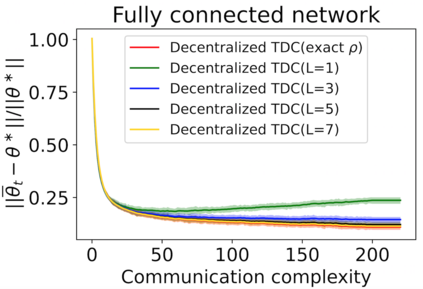
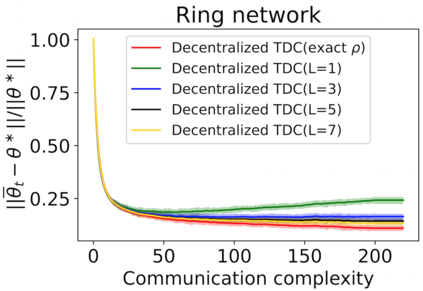
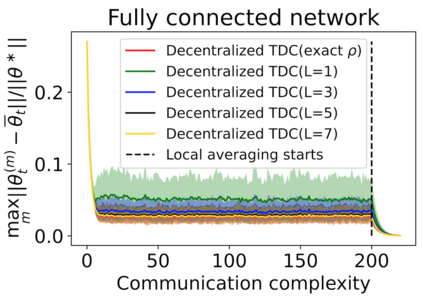
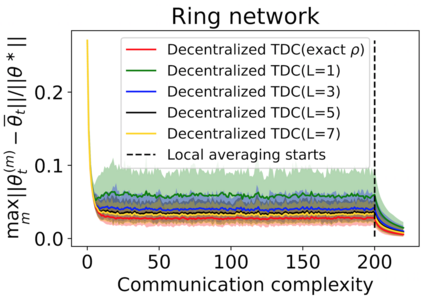
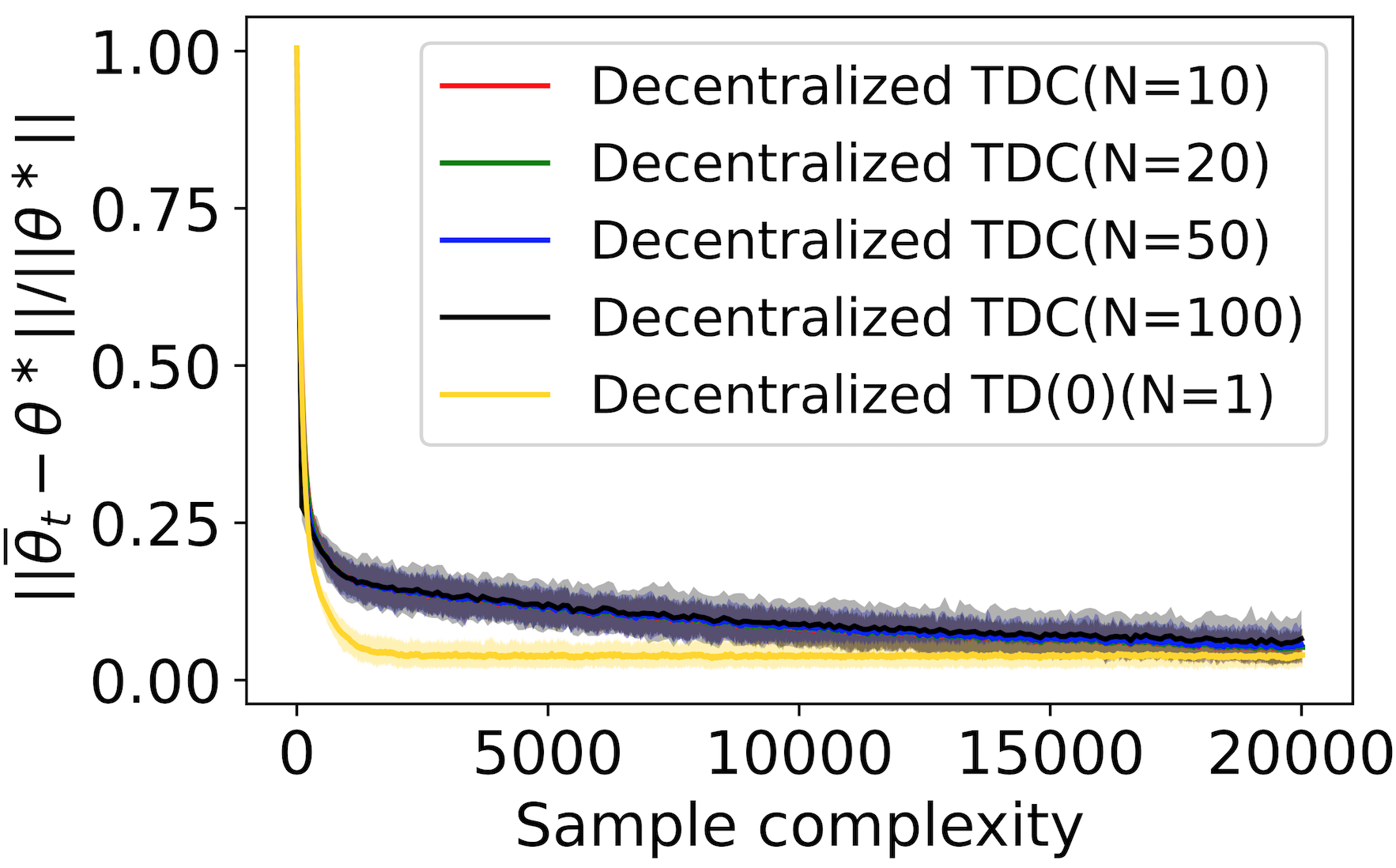
The finite-time convergence of off-policy TD learning has been comprehensively studied recently. However, such a type of convergence has not been well established for off-policy TD learning in the multi-agent setting, which covers broader applications and is fundamentally more challenging. This work develops two decentralized TD with correction (TDC) algorithms for multi-agent off-policy TD learning under Markovian sampling. In particular, our algorithms preserve full privacy of the actions, policies and rewards of the agents, and adopt mini-batch sampling to reduce the sampling variance and communication frequency. Under Markovian sampling and linear function approximation, we proved that the finite-time sample complexity of both algorithms for achieving an $\epsilon$-accurate solution is in the order of $\mathcal{O}(\epsilon^{-1}\ln \epsilon^{-1})$, matching the near-optimal sample complexity of centralized TD(0) and TDC. Importantly, the communication complexity of our algorithms is in the order of $\mathcal{O}(\ln \epsilon^{-1})$, which is significantly lower than the communication complexity $\mathcal{O}(\epsilon^{-1}\ln \epsilon^{-1})$ of the existing decentralized TD(0). Experiments corroborate our theoretical findings.
翻译:最近已全面研究了脱离政策的TD学习的有限时间趋同问题。然而,在多试剂环境下,这种非政策性TD学习的趋同类型还没有很好地确立,它涵盖更广泛的应用,而且更具挑战性。这项工作开发了两种分散的TD(TDC)算法,用于在Markovian抽样中进行多试剂脱离政策的TD学习。特别是,我们的算法保持了代理人行动、政策和奖励的充分隐私,并采用了微型批量抽样,以减少取样差异和通信频率。在Markovian抽样和线性函数近似之下,我们证明两种算法的有限时间抽样复杂性对于实现美元(epsilon$-acurate)的精确解决方案是按$\mathcal{O}(epsilon_1 ⁇ n =1}(eepsilon_lus%_lation__%xxxxxxxxxxxlisal_xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxl_____________xlalal_____xxxxxlislisl_xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx