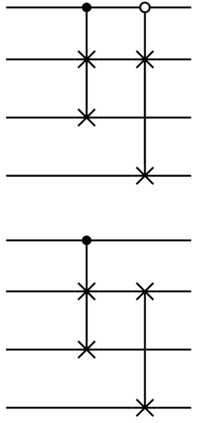
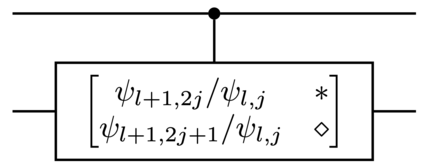
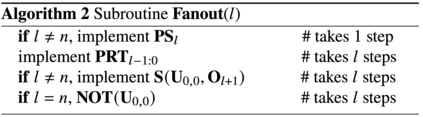
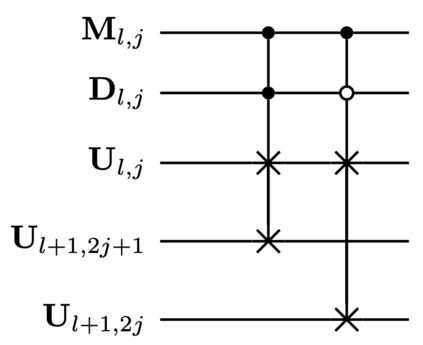
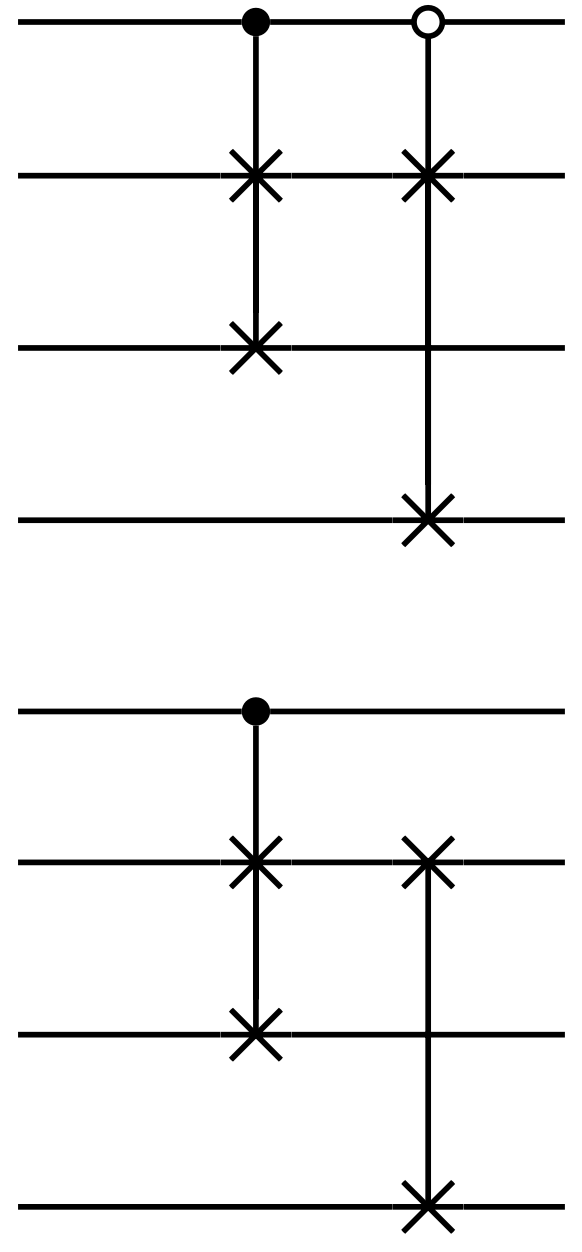
Quantum state preparation, as a general process of loading classical data to quantum device, is essential for end-to-end implementation of quantum algorithms. Yet, existing methods suffer from either high circuit depth or complicated hardware, limiting their practicality and robustness. In this work, we overcome these limitations with a bucket-brigade approach. The tree architectures of our hardware represents the simplest connectivity required for achieving sub-exponential circuit depth. Leveraging the bucket-brigade mechanism that can suppress the error propagation between different branches, our approach exhibit exponential improvement on the robustness compared to existing depth-optimal methods. More specifically, the infidelity scales as $O(\text{polylog}(N))$ with data size $N$, as oppose to $O(N)$ for conventional methods. Moreover, our approach is the first to simultaneously achieve linear Clifford$+T$ circuit depth, gate count number, and space-time allocation. These advancements offer the opportunity for processing big data in both near-term and fault-tolerant quantum devices.
翻译:暂无翻译