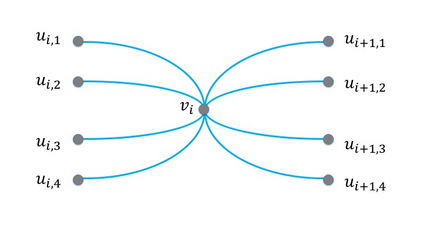
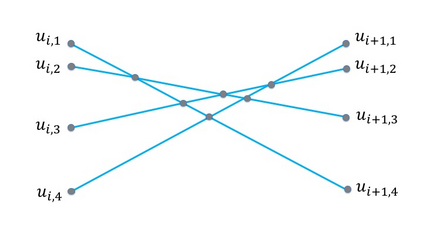
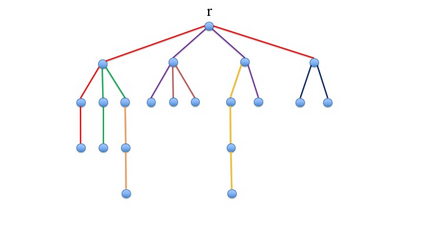
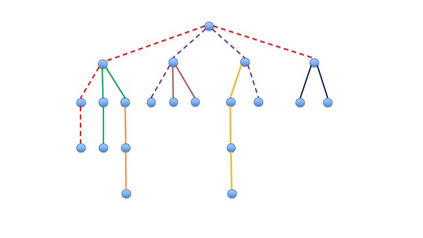
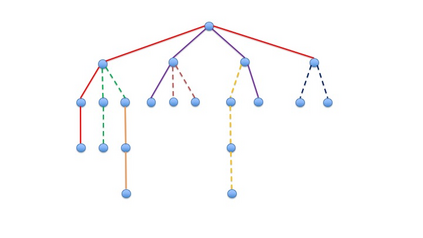
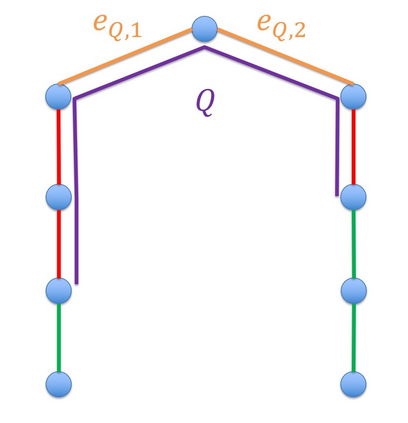
We study the worst-case welfare of item pricing in the \emph{tollbooth problem}. The problem was first introduced by Guruswami et al, and is a special case of the combinatorial auction in which (i) each of the $m$ items in the auction is an edge of some underlying graph; and (ii) each of the $n$ buyers is single-minded and only interested in buying all edges of a single path. We consider the competitive ratio between the hindsight optimal welfare and the optimal worst-case welfare among all item-pricing mechanisms, when the order of the arriving buyers is adversarial. We assume that buyers own the \emph{tie-breaking} power, i.e. they can choose whether or not to buy the demand path at 0 utility. We prove a tight competitive ratio of $3/2$ when the underlying graph is a single path (also known as the \emph{highway} problem), whereas item-pricing can achieve the hindsight optimal if the seller is allowed to choose a proper tie-breaking rule to maximize the welfare. Moreover, we prove an $O(1)$ upper bound of competitive ratio when the underlying graph is a tree. For general graphs, we prove an $\Omega(m^{1/8})$ lower bound of the competitive ratio. We show that an $m^{\Omega(1)}$ competitive ratio is unavoidable even if the graph is a grid, or if the capacity of every edge is augmented by a constant factor $c$. The results hold even if the seller has tie-breaking power.
翻译:我们研究了在 emph{tollbouth 问题中项目定价的最坏情况。 这个问题首先由 Guruswami 等人提出, 并且是组合拍卖中的一个特殊案例, 即:(一) 拍卖中每个百万美元的项目是某种基本图的边缘; 和 (二) 每个美元买家都是单心的, 并且只有兴趣购买单一路径的所有边缘。 我们考虑的是后见最佳福利和所有项目定价机制中最坏情况的最佳比率之间的竞争比率, 当即将到货的买主的订单是对立的。 我们假设买家拥有 &emph{tie-rebrea} 电力, 也就是说, 他们可以选择是否在0个实用图的边缘购买需求路径; 和 (二) 当基本图表是一条单一路径(也称为 emph{highway} 问题), 而如果允许卖主选择一个适当的断线规则以最大限度地提高福利。 (c) 价格的比值比值比值比值比值最高, 我们证明一个不变的正值是O 。