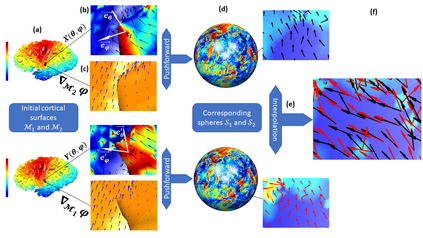
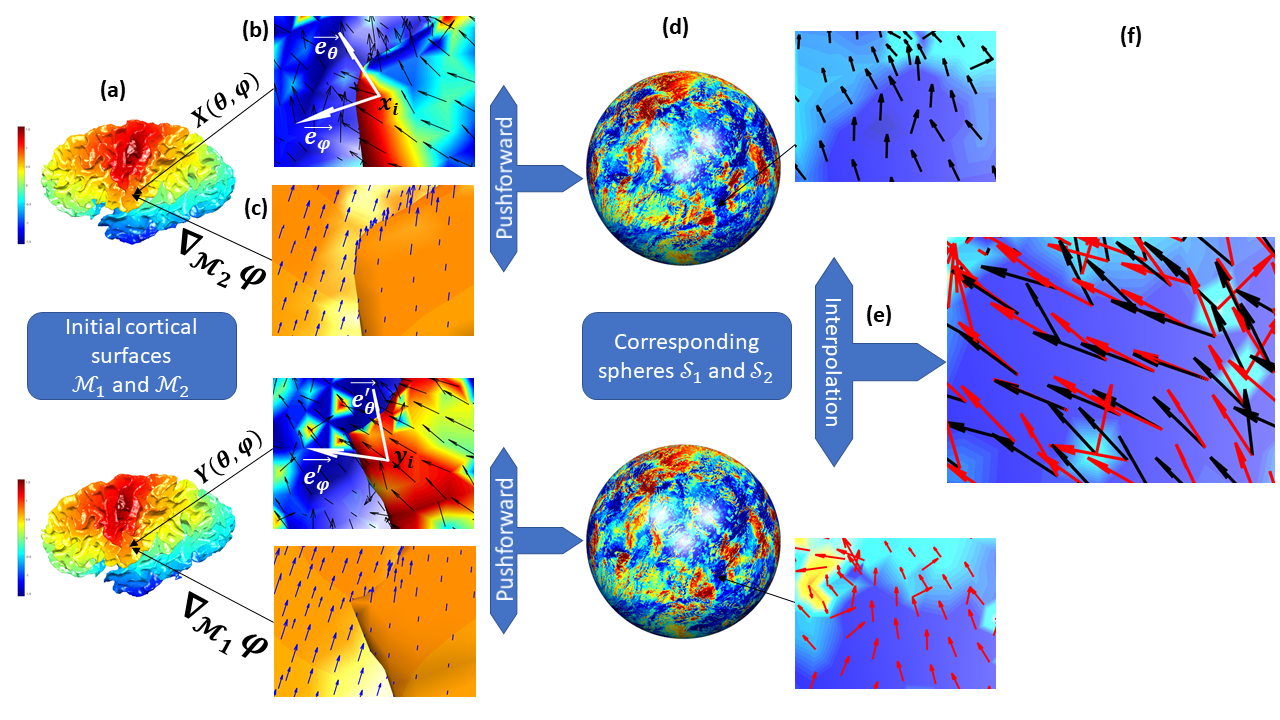
Vectors fields defined on surfaces constitute relevant and useful representations but are rarely used. One reason might be that comparing vector fields across two surfaces of the same genus is not trivial: it requires to transport the vector fields from the original surfaces onto a common domain. In this paper, we propose a framework to achieve this task by mapping the vector fields onto a common space, using some notions of differential geometry. The proposed framework enables the computation of statistics on vector fields. We demonstrate its interest in practice with an application on real data with a quantitative assessment of the reproducibility of curvature directions that describe the complex geometry of cortical folding patterns. The proposed framework is general and can be applied to different types of vector fields and surfaces, allowing for a large number of high potential applications in medical imaging.
翻译:在表面上定义的矢量字段是相关和有用的表示,但很少使用,原因之一可能是比较同一基因的两个表面的矢量字段并非微不足道:需要将矢量字段从原始表面迁移到一个共同领域。在本文件中,我们提出一个框架,通过利用差别几何概念将矢量字段映射到一个共同空间来完成这项任务。拟议框架有助于计算矢量字段的统计数据。我们通过应用真实数据,对描述复杂折叠模式的曲度方向的可复制性进行定量评估,来表明其在实践中的兴趣。拟议框架是一般性的,可以适用于不同种类的矢量字段和表面,允许在医学成像中大量的潜在应用。