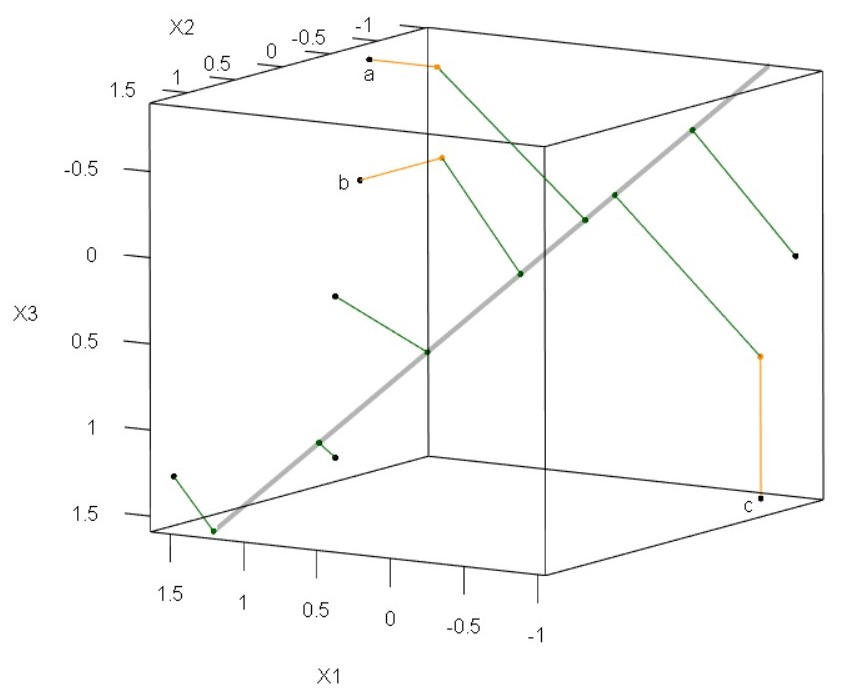
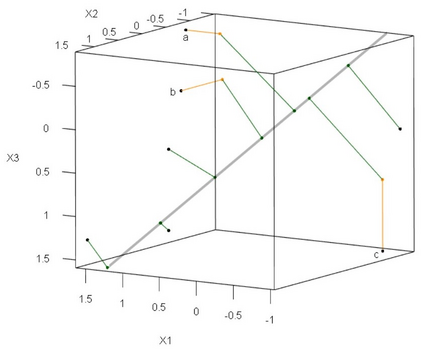
Principal component analysis (PCA) is a fundamental tool for analyzing multivariate data. Here the focus is on dimension reduction to the principal subspace, characterized by its projection matrix. The classical principal subspace can be strongly affected by the presence of outliers. Traditional robust approaches consider casewise outliers, that is, cases generated by an unspecified outlier distribution that differs from that of the clean cases. But there may also be cellwise outliers, which are suspicious entries that can occur anywhere in the data matrix. Another common issue is that some cells may be missing. This paper proposes a new robust PCA method, called cellPCA, that can simultaneously deal with casewise outliers, cellwise outliers, and missing cells. Its single objective function combines two robust loss functions, that together mitigate the effect of casewise and cellwise outliers. The objective function is minimized by an iteratively reweighted least squares (IRLS) algorithm. Residual cellmaps and enhanced outlier maps are proposed for outlier detection. The casewise and cellwise influence functions of the principal subspace are derived, and its asymptotic distribution is obtained. Extensive simulations and two real data examples illustrate the performance of cellPCA.
翻译:主成分分析(PCA)是处理多元数据的基础工具。本文聚焦于通过投影矩阵表征的主子空间降维问题。经典主子空间易受异常值影响。传统稳健方法主要针对个案异常值,即由与干净数据分布不同的异常分布生成的观测样本。然而,数据矩阵中任意位置可能出现的单元格异常值同样存在。此外,数据缺失也是常见问题。本文提出一种名为cellPCA的新型稳健PCA方法,可同步处理个案异常值、单元格异常值与缺失数据。其单一目标函数融合了两个稳健损失函数,共同抑制两类异常值的影响。该目标函数通过迭代再加权最小二乘(IRLS)算法实现最小化。研究提出了残差单元格图与增强型异常值图用于异常检测,推导了主子空间的个案与单元格影响函数,并获得了其渐近分布。大量模拟实验与两个真实数据案例验证了cellPCA的优越性能。