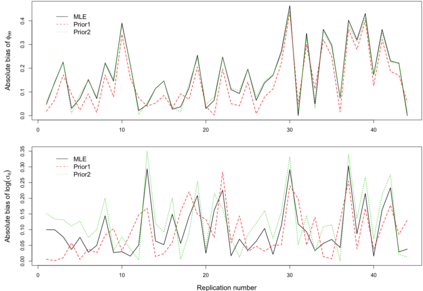
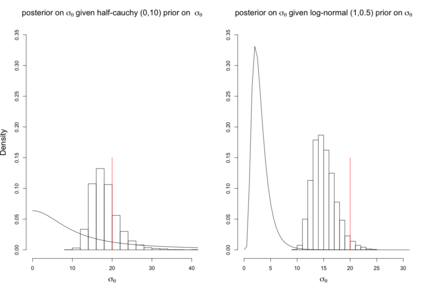
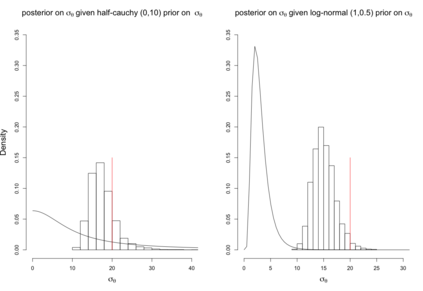
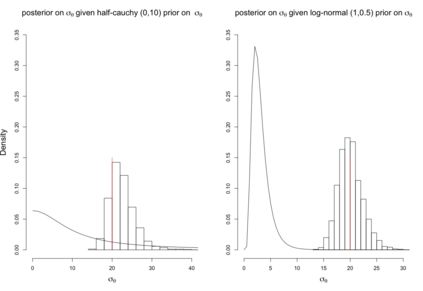
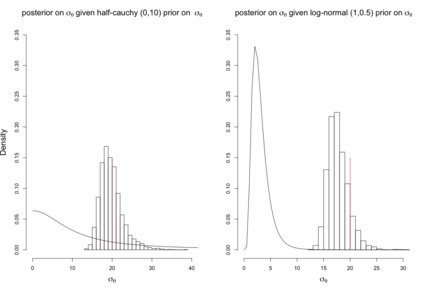
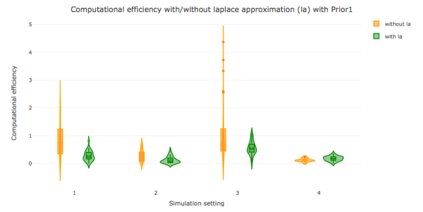
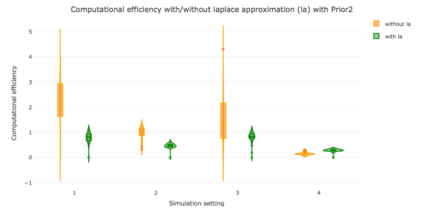
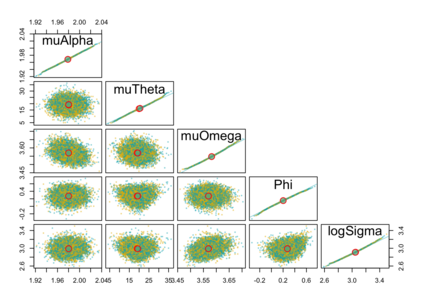
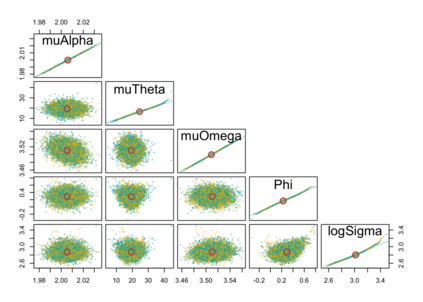
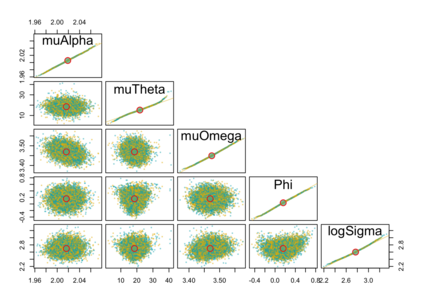
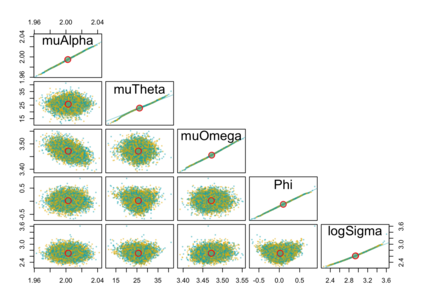
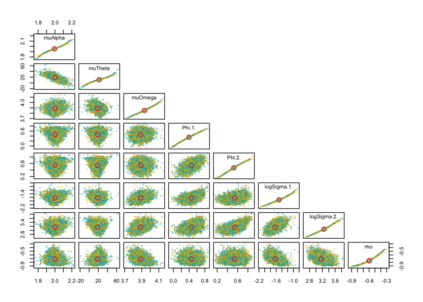
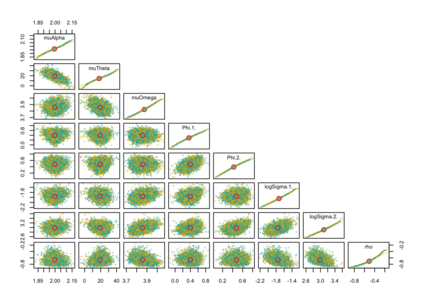
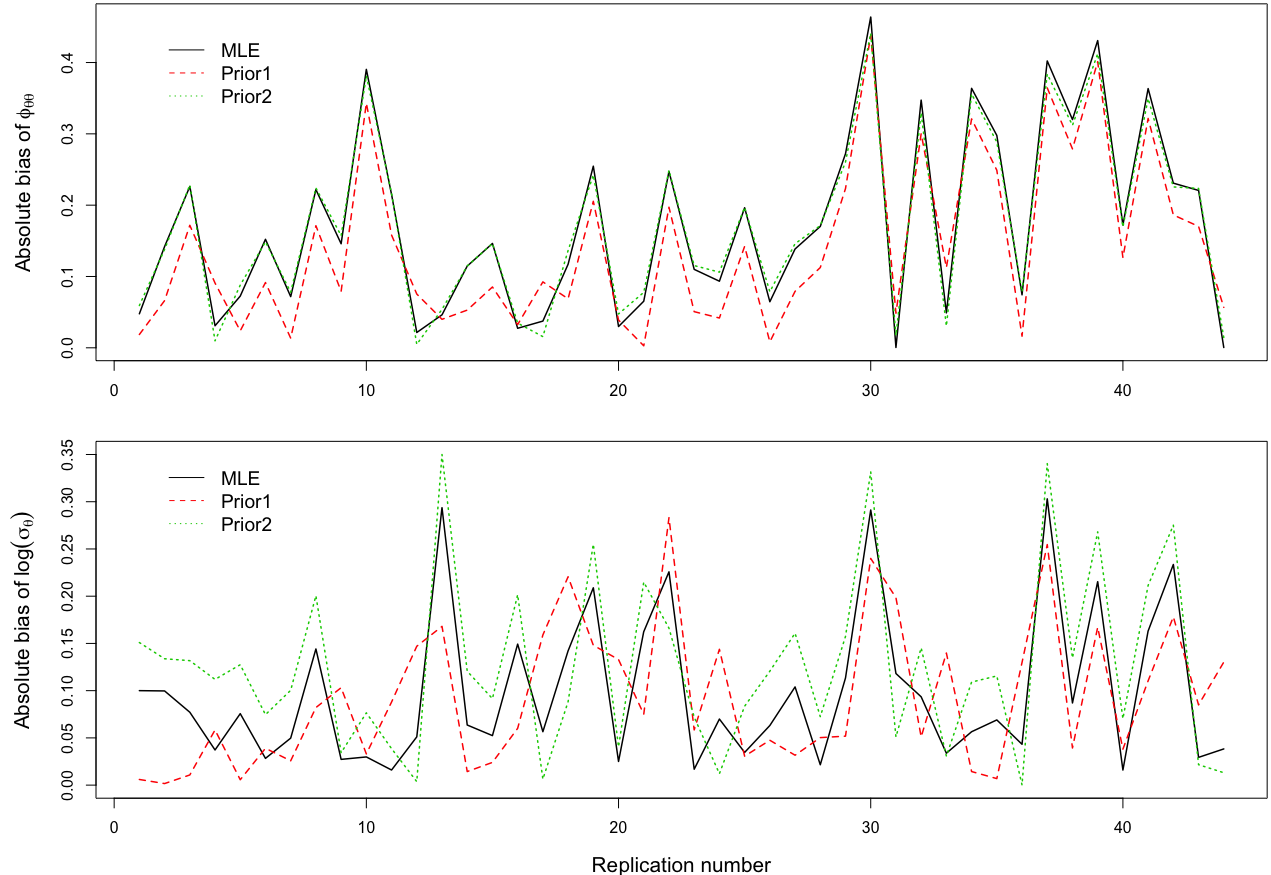
When using R package tmbstan for Bayesian inference, the built-in feature Laplace approximation to the marginal likelihood with random effects integrated out can be switched on and off. There exists no guideline on whether Laplace approximation should be used to achieve better efficiency especially when the statistical model for estimating selection is complicated. To answer this question, we conducted simulation studies under different scenarios with a state-space model employing a VAR(1) state equation. We found that turning on Laplace approximation in tmbstan would probably lower the computational efficiency, and only when there is a good amount of data, both tmbstan with and without Laplace approximation are worth trying since in this case, Laplace approximation is more likely to be accurate and may also lead to slightly higher computational efficiency. The transition parameters and scale parameters in a VAR(1) process are hard to be estimated accurately and increasing the sample size at each time point do not help in the estimation, only more time points in the data contain more information on these parameters and make the likelihood dominate the posterior likelihood, thus lead to accurate estimates for them.
翻译:使用 R 包件 tmbstan 进行巴耶斯语推断时, 内置的Laplace 近似值与 随机效应的边际可能性相近时, 可以开关。 对于是否应该使用 Laplace 近近似值来提高效率, 特别是在统计模型评估选择的复杂情况下。 回答这个问题, 我们在不同假设情景下进行了模拟研究, 使用VAR(1) 状态方程式使用州空间模型进行模拟研究。 我们发现, 在 tmbstan 中转用 Laplace 近似值可能会降低计算效率, 只有当数据数量充足时, 带有和没有Laplace 近似值的数据都值得尝试, 因为在这种情况下, Laplace 近似值更有可能准确, 并可能导致计算效率略高一点。 VAR(1) 过程中的过渡参数和比例参数很难准确估计, 提高每个时间点的样本大小无助于估计, 数据中只有更多的时间点含有关于这些参数的更多信息, 并有可能支配海图的可能性, 从而导致对它们进行准确的估计 。