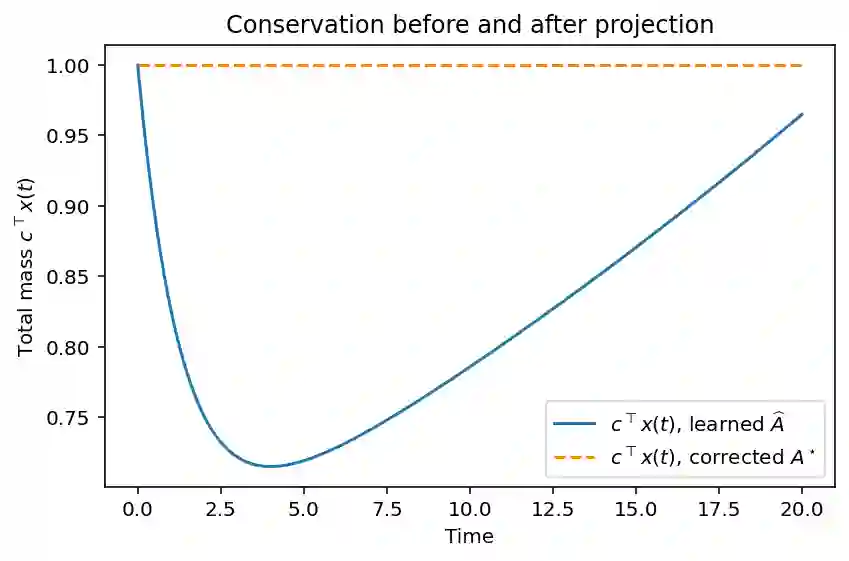
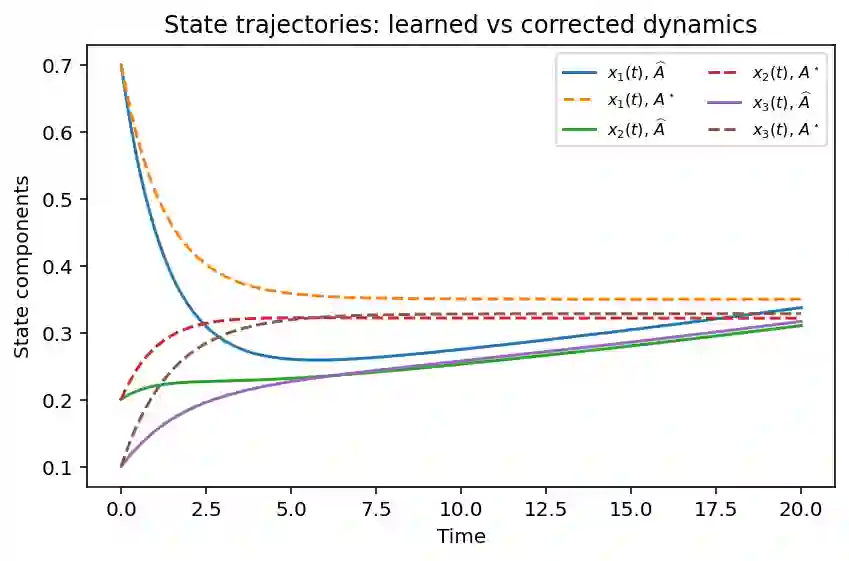
We consider the problem of restoring linear conservation laws in data-driven linear dynamical models. Given a learned operator $\widehat{A}$ and a full-rank constraint matrix $C$ encoding one or more invariants, we show that the matrix closest to $\widehat{A}$ in the Frobenius norm and satisfying $C^\top A = 0$ is the orthogonal projection $A^\star = \widehat{A} - C(C^\top C)^{-1}C^\top \widehat{A}$. This correction is uniquely defined, low rank and fully determined by the violation $C^\top \widehat{A}$. In the single-invariant case it reduces to a rank-one update. We prove that $A^\star$ enforces exact conservation while minimally perturbing the dynamics, and we verify these properties numerically on a Markov-type example. The projection provides an elementary and general mechanism for embedding exact invariants into any learned linear model.
翻译:我们考虑在数据驱动的线性动力学模型中恢复线性守恒律的问题。给定一个学习到的算子$\widehat{A}$和一个满秩约束矩阵$C$(编码一个或多个不变量),我们证明在Frobenius范数下最接近$\widehat{A}$且满足$C^\top A = 0$的矩阵是正交投影$A^\star = \widehat{A} - C(C^\top C)^{-1}C^\top \widehat{A}$。该修正项是唯一定义的、低秩的,并且完全由违反项$C^\top \widehat{A}$决定。在单不变量情况下,它简化为一个秩一更新。我们证明了$A^\star$能够在最小扰动动力学的同时强制执行精确守恒,并通过一个马尔可夫型示例对这些性质进行了数值验证。该投影提供了一种基础且通用的机制,用于将精确不变量嵌入到任何学习到的线性模型中。