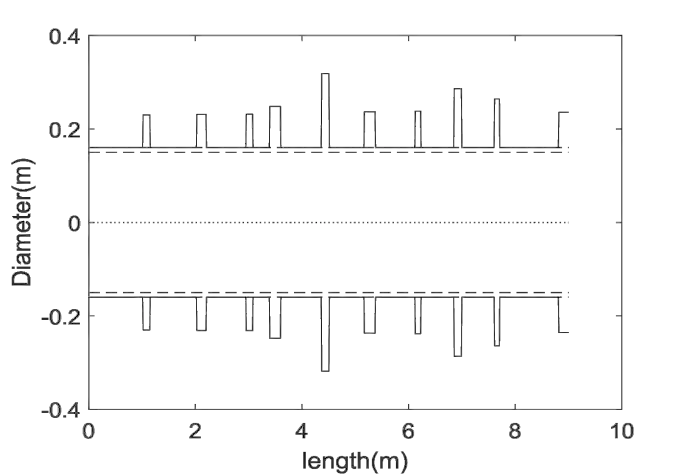
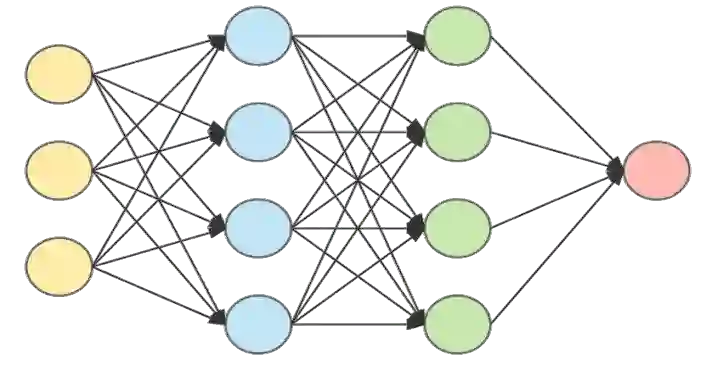
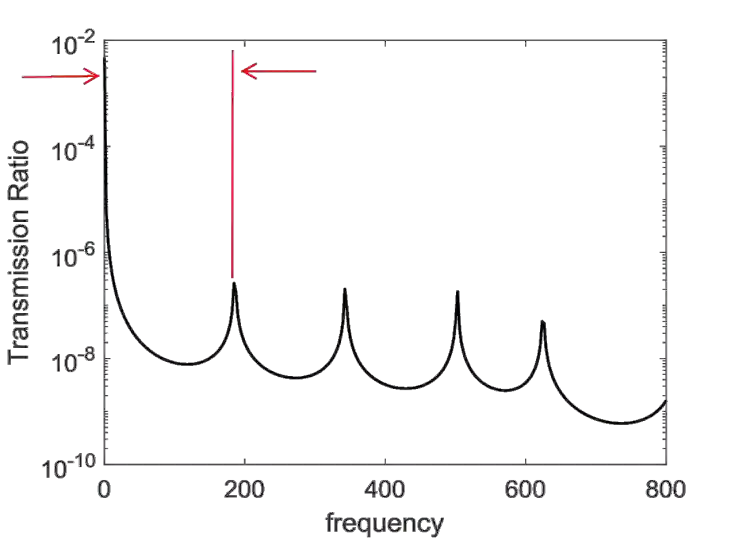
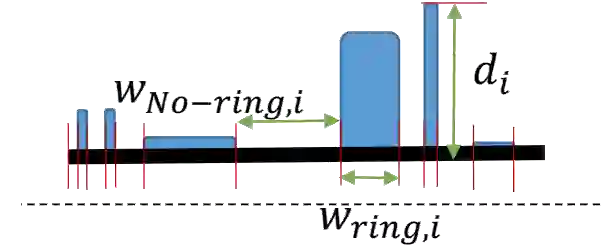
Aperiodic metamaterials represent a class of structural systems that are composed of different building blocks (cells), instead of a self-repeating chain of the same unit cells. Optimizing aperiodic cellular structural systems thus presents high-dimensional problems that are challenging to solve using purely high-fidelity structural optimization approaches. Specialized analytical modeling along with metamodel based optimization can provide a more tractable alternative solution approach. To this end, this paper presents a design automation framework applied to a 1D metamaterial system, namely a drill string, where vibration suppression is of utmost importance. The drill string comprises a set of nonuniform rings attached to the outer surface of a longitudinal rod. As such, the resultant system can now be perceived as an aperiodic 1D metamaterial with each ring/gap representing a cell. Despite being a 1D system, the simultaneous consideration of multiple DoF (i.e., torsional, axial, and lateral motions) poses significant computational challenges. Therefore, a transfer matrix method (TMM) is employed to analytically determine the frequency response of the drill string. A suite of neural networks (ANN) is trained on TMM samples (which present minute-scale computing costs per evaluation), to model the frequency response. ANN-based optimization is then performed to minimize mass subject to constraints on the gap between consecutive resonance peaks in one case, and minimizing this gap in the second case, leading to crucial improvements over baselines. Further novel contribution occurs through the development of an inverse modeling approach that can instantaneously produce the 1D metamaterial design with minimum mass for a given desired non-resonant frequency range. This is accomplished by using invertible neural networks, and results show promising alignment with forward solutions.
翻译:定期元材料是一组结构系统,由不同的构件(细胞)组成,而不是同一单元细胞的自反应链。优化周期性细胞结构系统因此提出了高层面的问题,使用纯粹高不忠实的结构优化方法解决这些困难。专门的分析模型和基于元模的优化可以提供一个更易移动的替代解决方案。为此,本文件提出了一个适用于1D元材料系统的设计自动化框架,即一个钻线,其中振动抑制是最重要的。钻线由一组连接同一单元细胞的外表面的不统一星际环组成。优化一个周期性细胞结构系统,因此,由此产生的系统现在被视为一个周期性1D元材料,每个环/格都代表一个细胞。尽管是一个 1D 系统,但同时考虑多个DF(即感官、xion、xialalal和olalsmoal 动作) 构成了重大的计算挑战。因此,一个转移矩阵法方法(TMMM) 用于分析这一钻头1 最低频率网络的不统一频率反应,一个经过测试的神经模型到当前一个模型的模型的模型,一个运行中,一个模型显示一个模型到一个模型的模型的模型的模型的模型到一个模型的模型的模型的模型到一个模型的模型的模型的模型的模型到一个模型的模型的模型的模型的模型的模型的模型的模型的模型到现在的模型到现在的模型的模型的模型的模型到一个模型的模型的模型的模型的模型的模型到一个模型的模型的模型的模型。