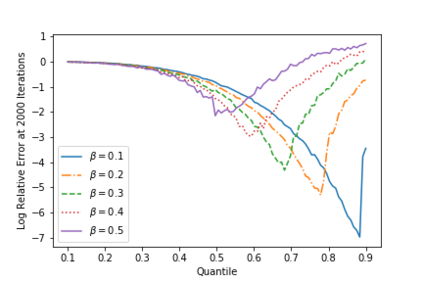
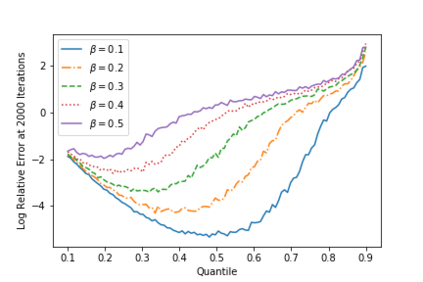
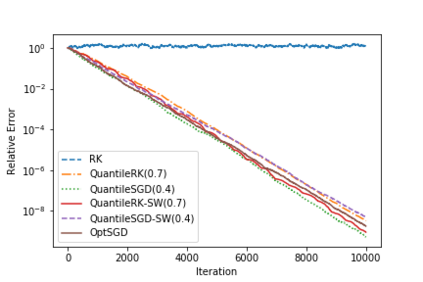
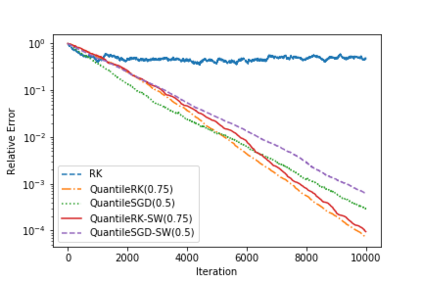
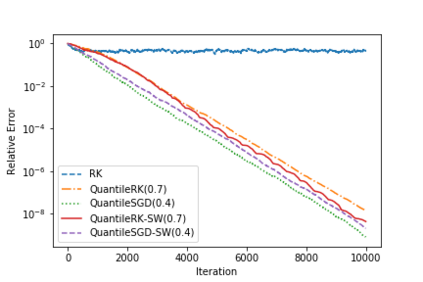
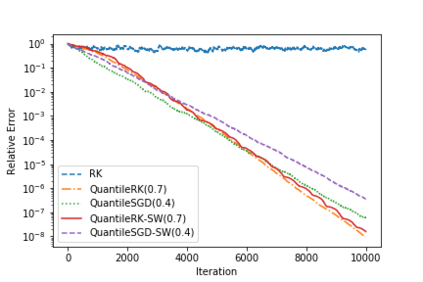
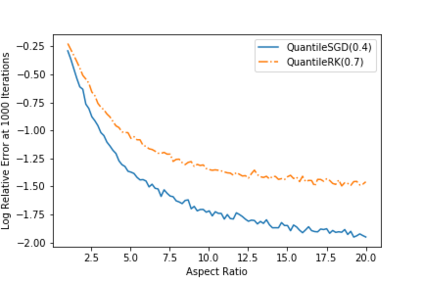
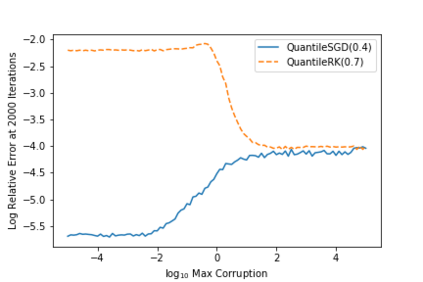
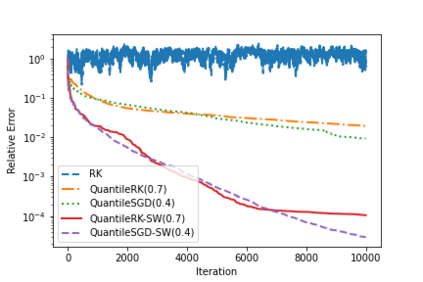
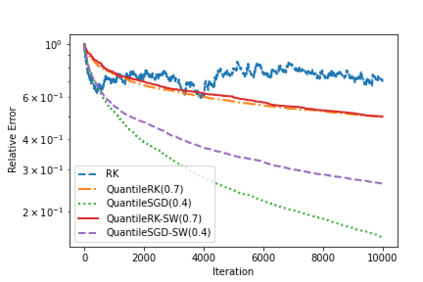
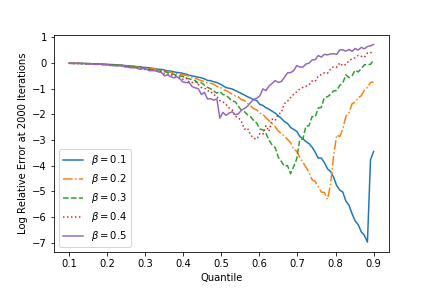
Often in applications ranging from medical imaging and sensor networks to error correction and data science (and beyond), one needs to solve large-scale linear systems in which a fraction of the measurements have been corrupted. We consider solving such large-scale systems of linear equations $\mathbf{A}\mathbf{x}=\mathbf{b}$ that are inconsistent due to corruptions in the measurement vector $\mathbf{b}$. We develop several variants of iterative methods that converge to the solution of the uncorrupted system of equations, even in the presence of large corruptions. These methods make use of a quantile of the absolute values of the residual vector in determining the iterate update. We present both theoretical and empirical results that demonstrate the promise of these iterative approaches.
翻译:从医学成像和传感器网络到错误校正和数据科学(及以后)等应用,人们往往需要解决部分测量工作被破坏的大规模线性系统。我们考虑解决由于测量矢量$\mathbf{x ⁇ mathbf{x ⁇ mathbf{b{b}}美元方面的腐败而不一致的大型线性等式系统。我们开发了一些迭代方法的变种,这些变种可汇合到无干扰的方程式系统的解决办法中,即使在出现大规模腐败的情况下也是如此。这些方法利用残余矢量绝对值的四分法来确定循环更新。我们提出了理论和实验结果,显示了这些迭代方法的希望。