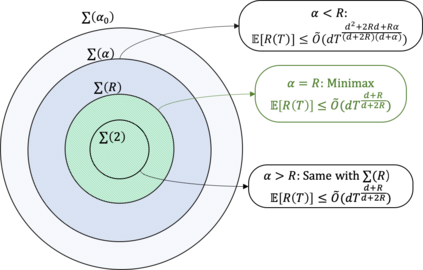
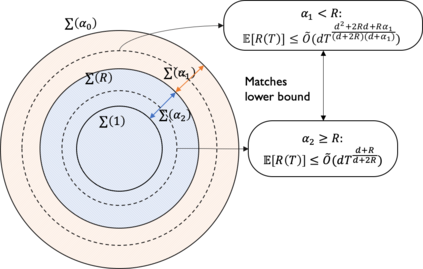
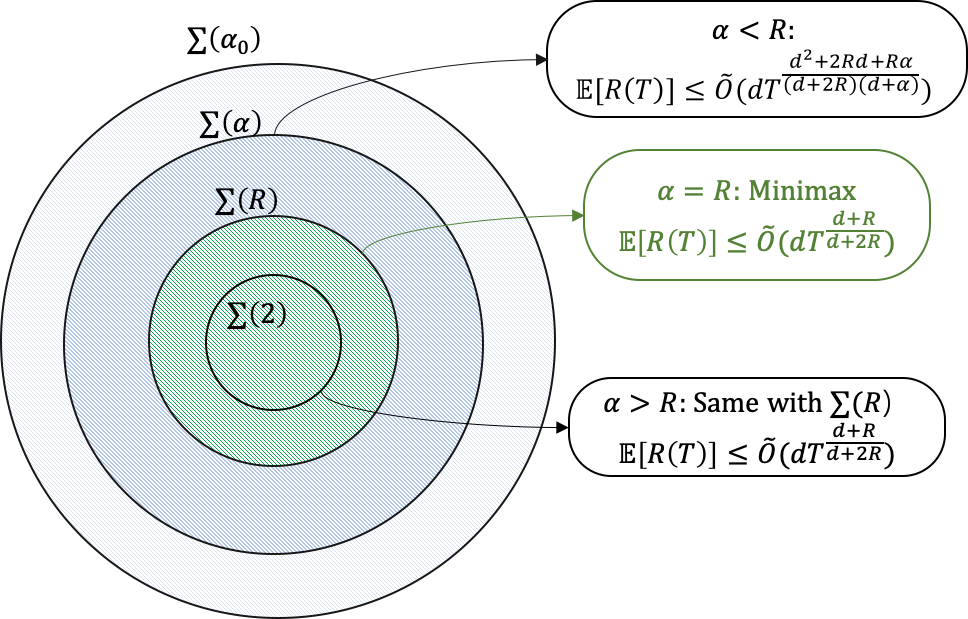
We consider bandit optimization of a smooth reward function, where the goal is cumulative regret minimization. This problem has been studied for $\alpha$-H\"older continuous (including Lipschitz) functions with $0<\alpha\leq 1$. Our main result is in generalization of the reward function to H\"older space with exponent $\alpha>1$ to bridge the gap between Lipschitz bandits and infinitely-differentiable models such as linear bandits. For H\"older continuous functions, approaches based on random sampling in bins of a discretized domain suffices as optimal. In contrast, we propose a class of two-layer algorithms that deploy misspecified linear/polynomial bandit algorithms in bins. We demonstrate that the proposed algorithm can exploit higher-order smoothness of the function by deriving a regret upper bound of $\tilde{O}(T^\frac{d+\alpha}{d+2\alpha})$ for when $\alpha>1$, which matches existing lower bound. We also study adaptation to unknown function smoothness over a continuous scale of H\"older spaces indexed by $\alpha$, with a bandit model selection approach applied with our proposed two-layer algorithms. We show that it achieves regret rate that matches the existing lower bound for adaptation within the $\alpha\leq 1$ subset.
翻译:我们考虑对一个光滑的奖励功能优化土匪, 目标是累积最小遗憾。 这个问题已经用$0 ⁇ alpha$- H\\\"老化连续功能( 包括Lipschitz) 来研究。 我们的主要结果是将奖励功能推广到 H\"老化空间, 以Expententententent $\alpha> 1$来缩小利普西茨土匪和线性土匪等无限差异型模型之间的差距。 对于 H\\"老式连续功能, 基于在离散域的垃圾桶中随机取样的方法是最佳的。 相比之下, 我们提出在垃圾桶中部署错误指定的线性/ 线性/ 线性强力算的连续功能( 包括利普西茨) 。 我们证明, 拟议的算法可以利用更高层次的平滑度功能, 使 $\\\\ d\ d\ d\ d\ d\\\\\\\\\\\\ alpha} $( $) 在 $\ alpha} 当 AL\\ a lax lax a le modeal press press 匹配时, 我们研究如何调整 内如何适应未知的模型, 一种不为1\\\\\ lax lax lax lax a 。 我们的模型的模型的模型的模型选择。