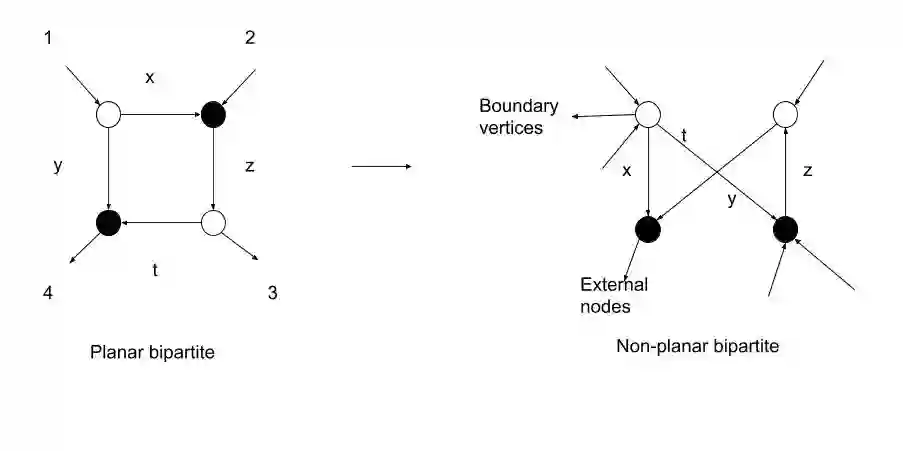
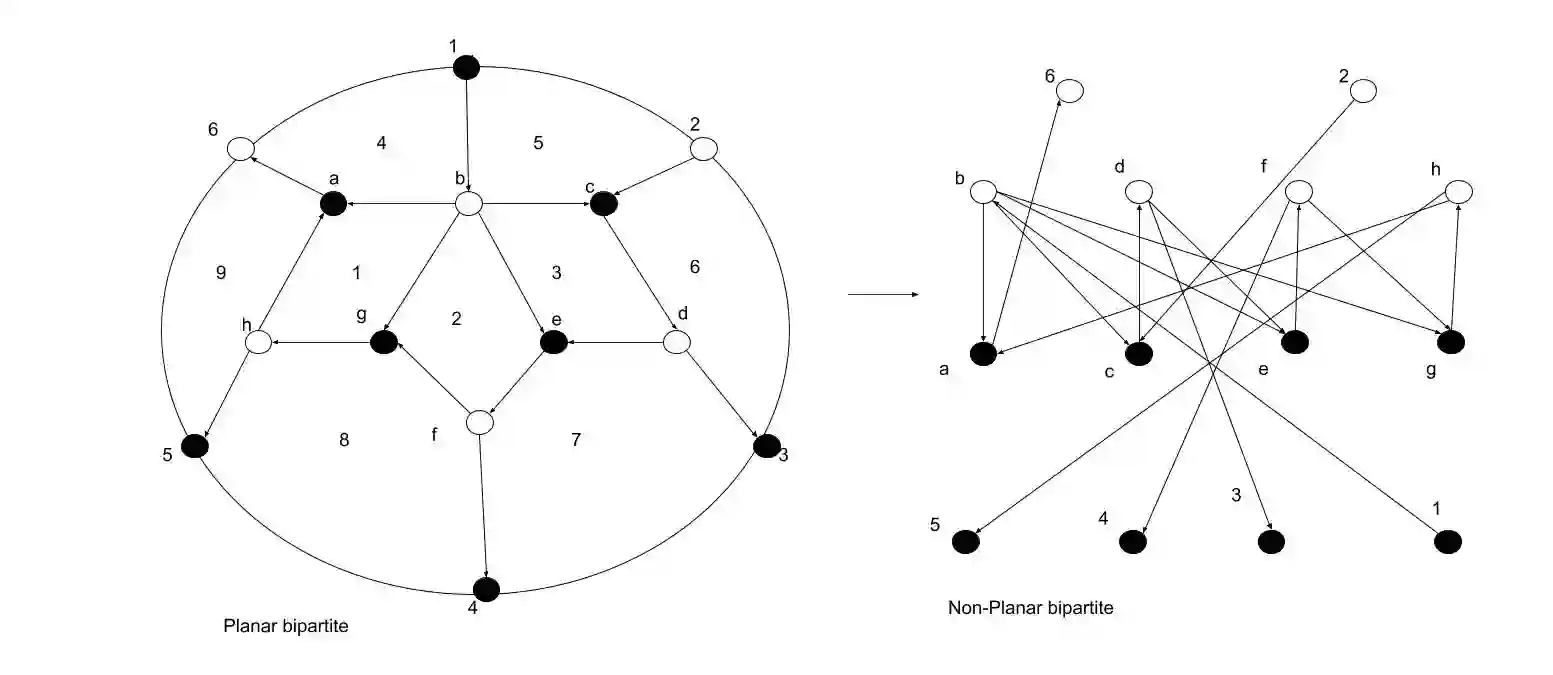
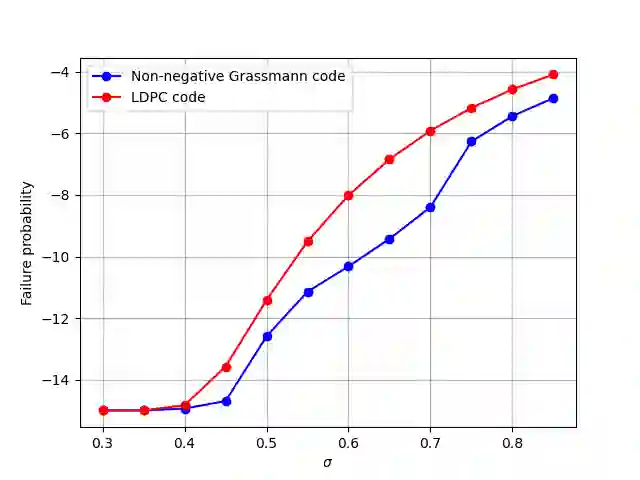
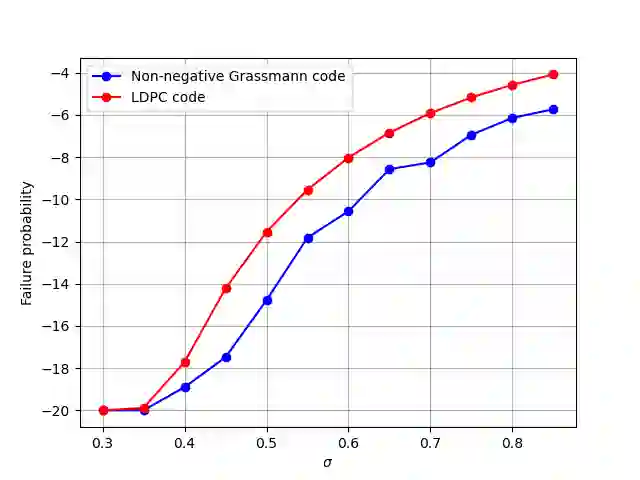
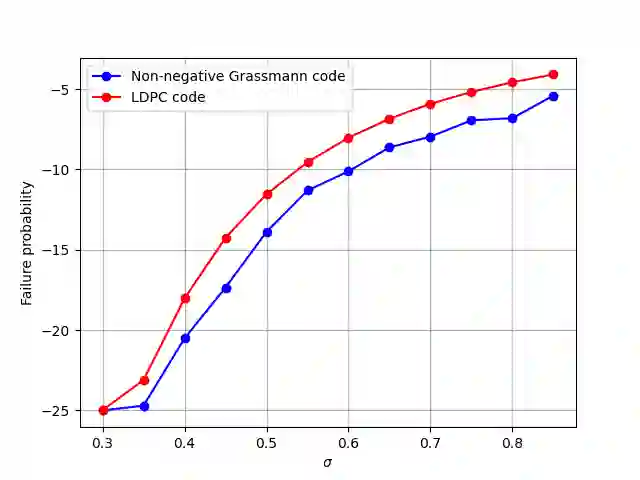
The syndrome decoding problem has been proposed as a computational hardness assumption for code based cryptosystem that are safe against quantum computing. The problem has been reduced to finding the codeword with the smallest non-zero columns that would satisfy a linear check equation. Variants of Information set decoding algorithms has been developed as cryptanalytic tools to solve the problem. In this paper, we study and generalize the solution to codes associated with the totally non-negative Grassmannian in the Grassmann metric. This is achieved by reducing it to an instance of finding a subset of the plucker coordinates with the smallest number of columns. Subsequently, the theory of the totally non negative Grassmann is extended to connect the concept of boundary measurement map to Tanner graph like code construction while deriving new analytical bounds on its parameters. The derived bounds shows that the complexity scales up on the size of the plucker coordinates. Finally, experimental results on decoding failure probability and complexity based on row operations are presented and compared to Low Density parity check codes in the Hamming metric.
翻译:综合解码问题被提议为基于代码的加密系统的一种计算硬度假设,这种密码系统对量子计算来说是安全的。 问题已被简化为找到使用最小的非零列的编码词, 从而满足线性检查方程式。 信息集解码算法的变体已发展成解码工具, 以解决这个问题。 在本文中, 我们研究并概括了格拉斯曼标准中与完全非阴性的格拉斯曼人相关的编码的解决方案。 其实现方式是将其降低到一个实例, 用最小数的列来找到一个提取器坐标的子子。 随后, 完全非负格拉斯曼的理论被扩展为将边界测量地图的概念与坦纳图的代码构造联系起来, 同时根据参数得出新的分析界限。 衍生的界限显示, 提取器坐标大小的复杂尺度。 最后, 基于行操作的解码概率和复杂性的实验结果被提出, 与哈明标准中的低密度对等校码比较。