New heuristic to choose a cylindrical algebraic decomposition variable ordering motivated by complexity analysis

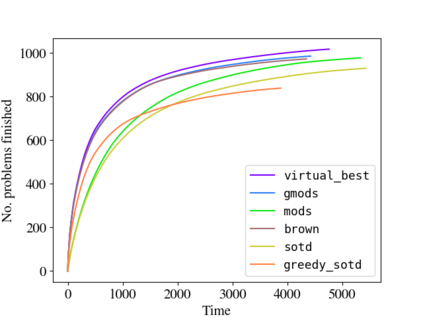
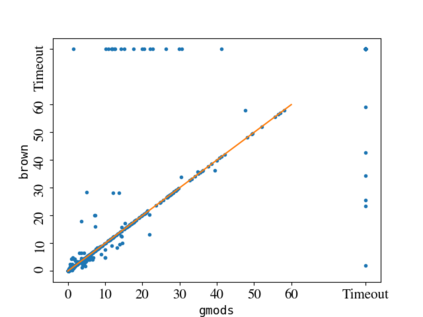
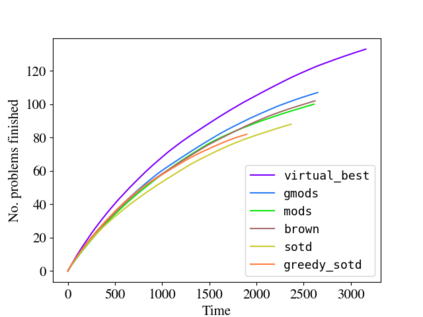
It is well known that the variable ordering can be critical to the efficiency or even tractability of the cylindrical algebraic decomposition (CAD) algorithm. We propose new heuristics inspired by complexity analysis of CAD to choose the variable ordering. These heuristics are evaluated against existing heuristics with experiments on the SMT-LIB benchmarks using both existing performance metrics and a new metric we propose for the problem at hand. The best of these new heuristics chooses orderings that lead to timings on average 17% slower than the virtual-best: an improvement compared to the prior state-of-the-art which achieved timings 25% slower.