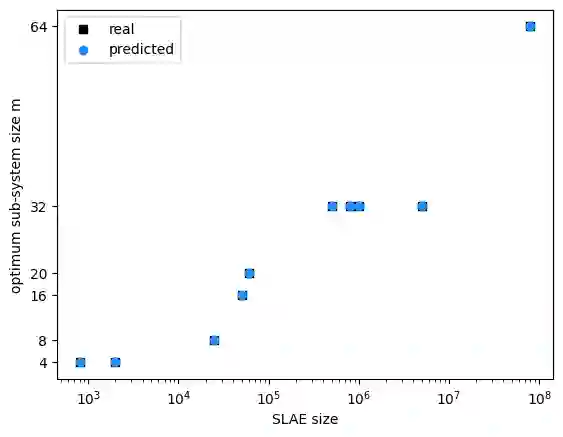
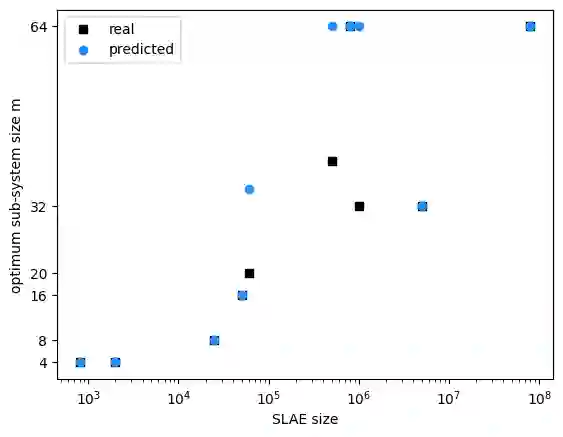
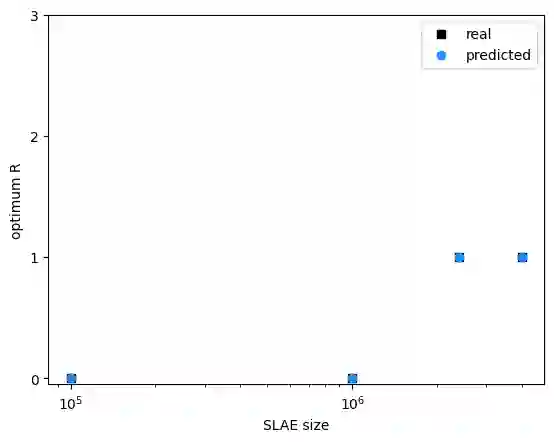
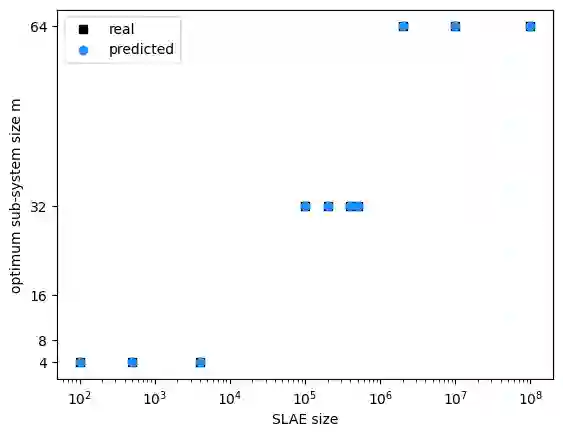
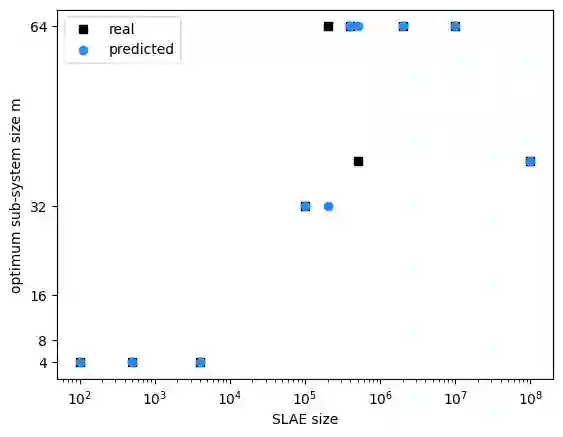
This paper presents a machine learning (ML)-based heuristic for finding the optimum sub-system size for the CUDA implementation of the parallel partition algorithm. Computational experiments for different system of linear algebraic equation (SLAE) sizes are conducted, and the optimum sub-system size for each of them is found empirically. To estimate a model for the sub-system size, we perform the k-nearest neighbors (kNN) classification method. Statistical analysis of the results is done. By comparing the predicted values with the actual data, the algorithm is deemed to be acceptably good. Next, the heuristic is expanded to work for the recursive parallel partition algorithm as well. An algorithm for determining the optimum sub-system size for each recursive step is formulated. A kNN model for predicting the optimum number of recursive steps for a particular SLAE size is built.
翻译:本文提出了一种基于机器学习(ML)的启发式方法,用于寻找并行划分算法CUDA实现中的最优子系统规模。针对不同规模的线性代数方程组(SLAE)进行了计算实验,并通过经验方法确定了各自的最优子系统规模。为构建子系统规模的预测模型,我们采用了k近邻(kNN)分类方法,并对结果进行了统计分析。通过比较预测值与实际数据,该算法被认定为具有可接受的优良性能。随后,该启发式方法被扩展至适用于递归并行划分算法。我们提出了一种用于确定各递归步骤最优子系统规模的算法,并构建了kNN模型以预测特定SLAE规模下的最优递归步骤数量。