Constructing Driver Hamiltonians for Several Linear Constraints

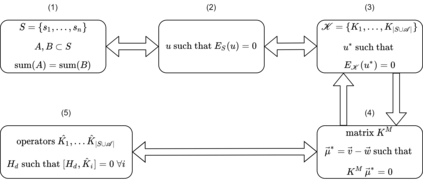
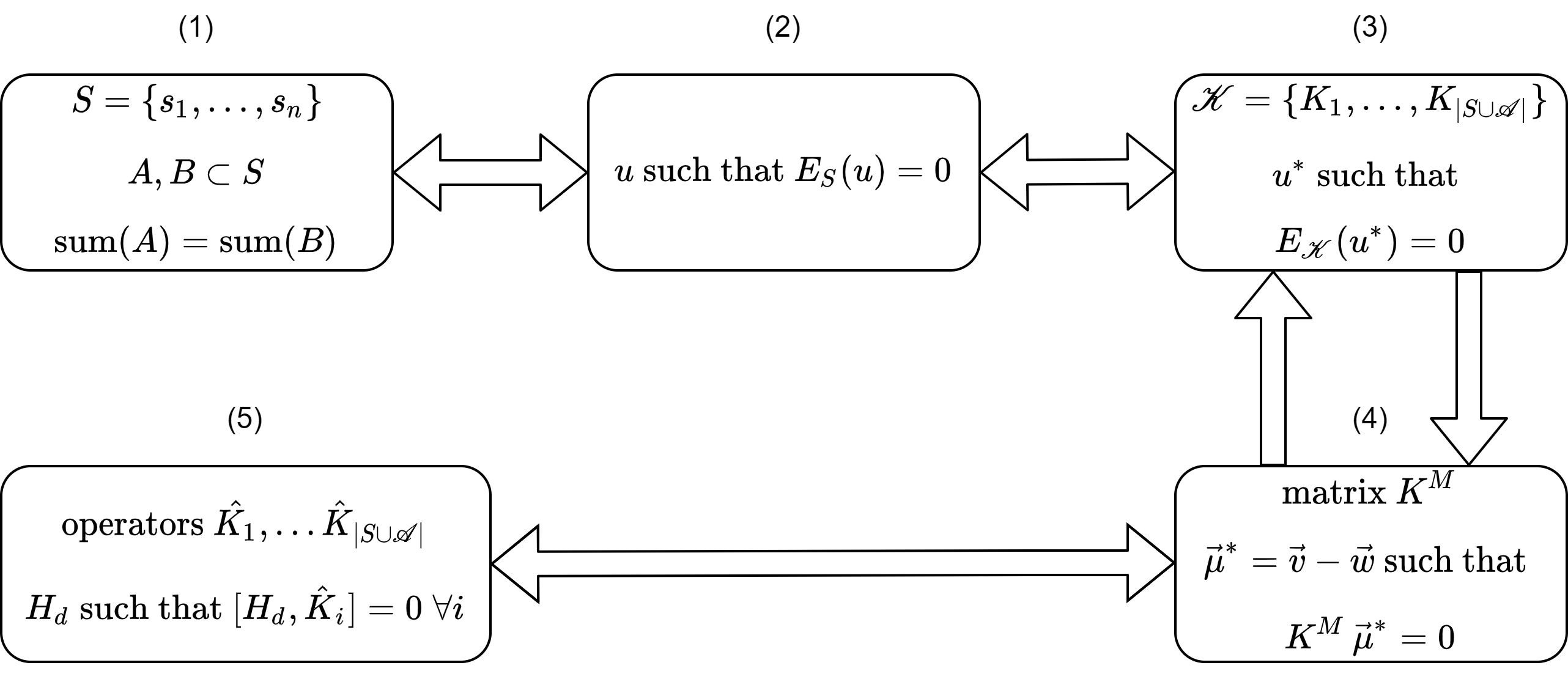
Recent advances in the field of adiabatic quantum computing and the closely related field of quantum annealers has centered around using more advanced and novel Hamiltonian representations to solve optimization problems. One of these advances has centered around the development of driver Hamiltonians that commute with the constraints of an optimization problem - allowing for another avenue to satisfying those constraints instead of imposing penalty terms for each of them. In particular, the approach is able to use sparser connectivity to embed several practical problems on quantum devices than other common practices. However, designing the driver Hamiltonians that successfully commute with several constraints has largely been based on strong intuition for specific problems and with no simple general algorithm to generate them for arbitrary constraints. In this work, we develop a simple and intuitive algebraic framework for reasoning about the commutation of Hamiltonians with linear constraints - one that allows us to classify the complexity of finding a driver Hamiltonian for an arbitrary set of constraints as NP-Complete.