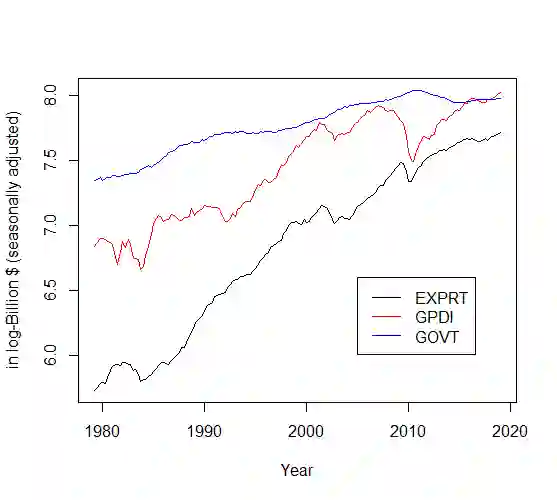
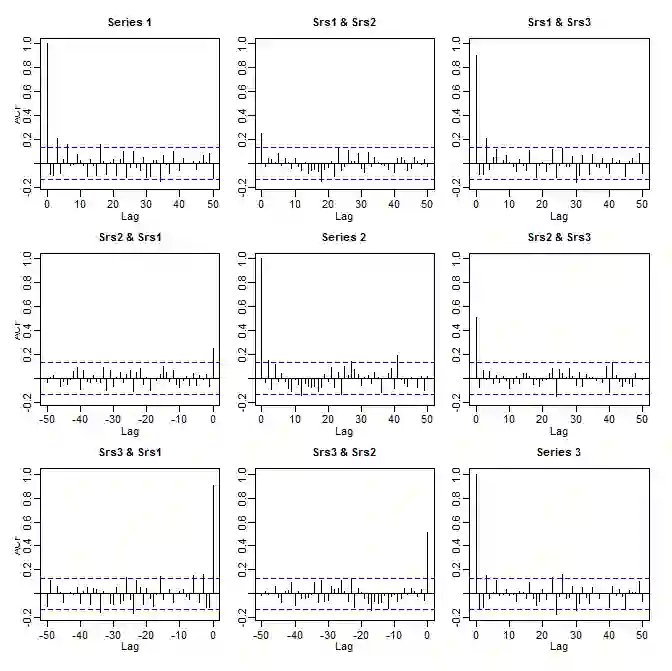
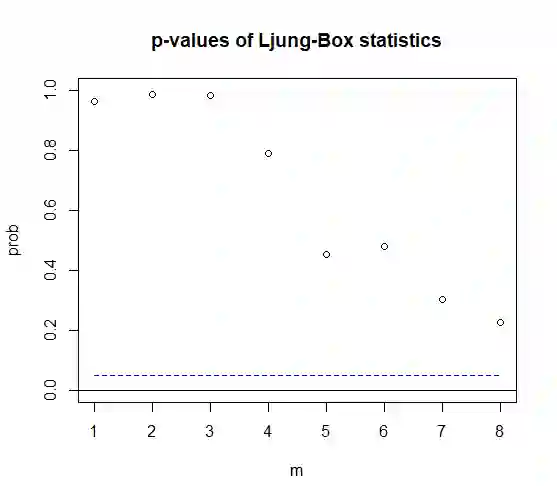
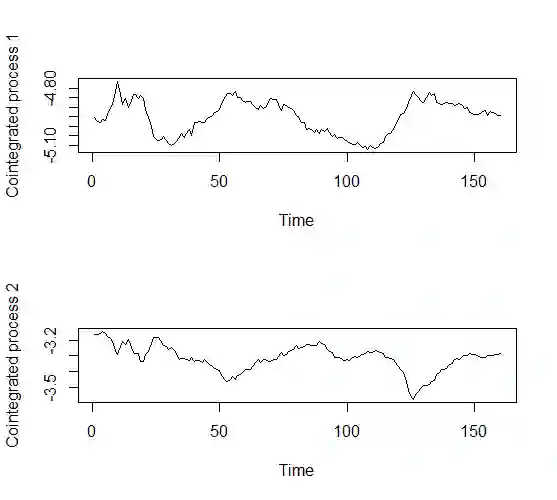
The paper provides a parametrization of Vector Autoregression (VAR) that enables one to look at the parameters associated with unit root dynamics and those associated with stable dynamics separately. The task is achieved via a novel factorization of the VAR polynomial that partitions the polynomial spectrum into unit root and stable and zero roots via polynomial factors. The proposed factorization adds to the literature of spectral factorization of matrix polynomials. The main benefit is that using the parameterization, actions could be taken to model the dynamics due to a particular class of roots, e.g. unit roots or zero roots, without changing the properties of the dynamics due to other roots. For example, using the parameterization one is able to estimate cointegrating space with appropriate rank that maintains the root structure of the original VAR processes or one can estimate a reduced rank causal VAR process maintaining the constraints of causality. In essence, this parameterization provides the practitioner an option to perform estimation of VAR processes with constrained root structure (e.g., conintegrated VAR or reduced rank VAR) such that the estimated model maintains the assumed root structure.
翻译:本文提供了矢量自动递减(VAR)的参数的平衡,使人们能够分别查看与单位根动态相关的参数和与稳定动态相关的参数。任务通过VAR多元值的新因素化完成,通过多元系数将多元光谱分割成单位根和稳定与零根。提议的系数化为矩阵多义的光谱分系数化文献增加了矩阵多义的文献内容。主要的好处是,使用参数化,可以采取行动模拟因某一类根(如单位根或零根)而导致的动态,而不必改变因其他根而导致的动态特性。例如,使用参数化一能够估计空间与维持原始VAR进程根结构的适当等级相融合,或能够估计维持因因因果关系限制而降低的因果性VAR进程。实质上,这一参数化为从业人员提供了一种选择,以对受根结构制约的VAR进程进行估计(例如,混成VAR或降为VAR级),这样估计模型就可以维持假定的根结构。