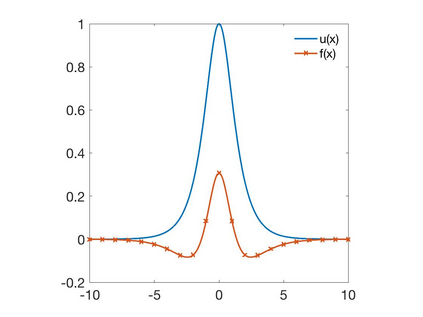
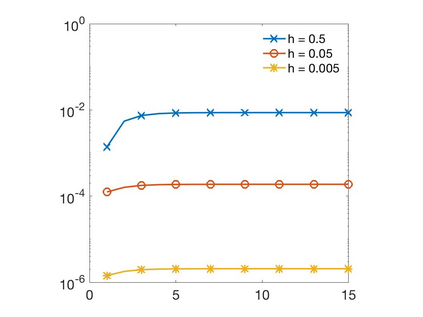
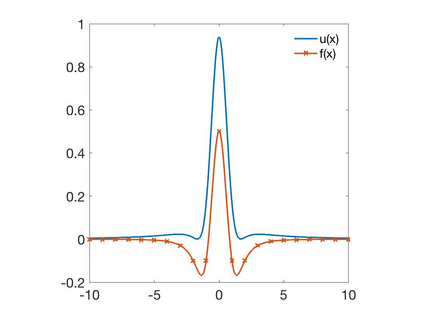
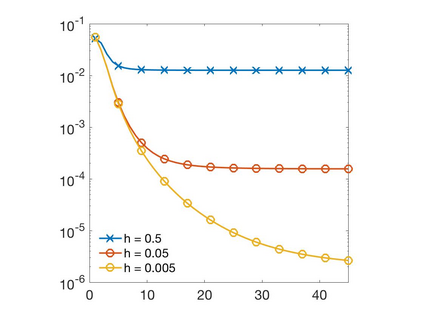
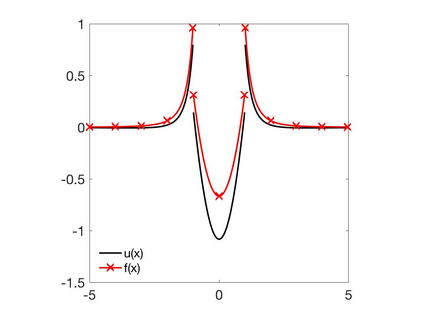
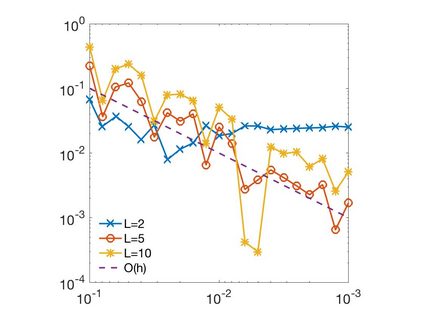
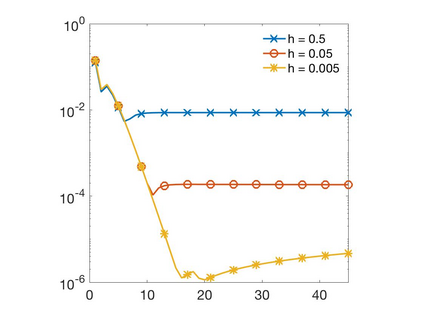
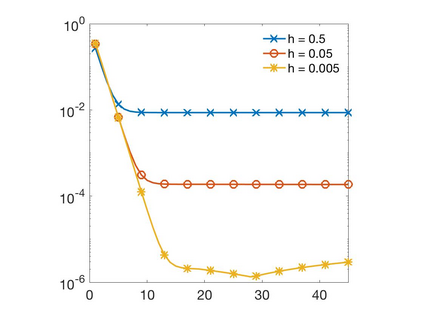
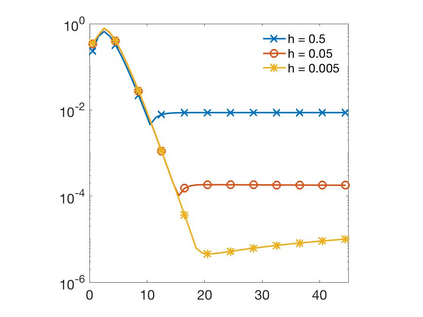
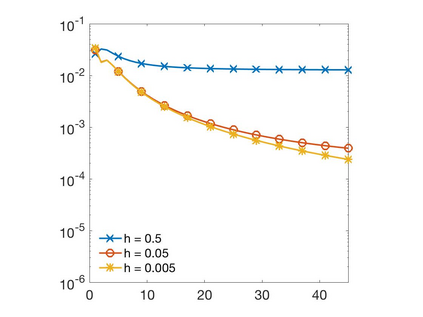
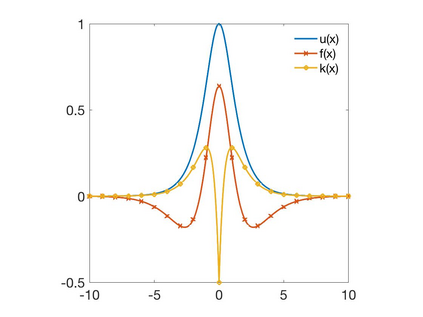
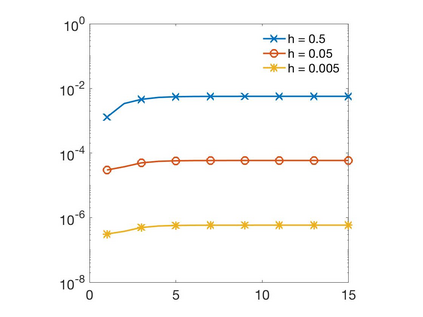
In this paper we develop a numerical scheme based on quadratures to approximate solutions of integro-differential equations involving convolution kernels, $\nu$, of diffusive type. In particular, we assume $\nu$ is symmetric and exponentially decaying at infinity. We consider problems posed in bounded domains and in $\R$. In the case of bounded domains with nonlocal Dirichlet boundary conditions, we show the convergence of the scheme for kernels that have positive tails, but that can take on negative values. When the equations are posed on all of $\R$, we show that our scheme converges for nonnegative kernels. Since nonlocal Neumann boundary conditions lead to an equivalent formulation as in the unbounded case, we show that these last results also apply to the Neumann problem.
翻译:在本文中,我们开发了一个基于二次方块的数值方案,以近似解决涉及共变内核的异式内核的异式方程式的近似解决办法为基础。我们特别假设$nu是对称性的,无穷无尽的指数衰减。我们考虑了在受约束域和以$/R美元构成的问题。在与非本地的Drichlet边界条件交界域的情况下,我们展示了具有正反面的内核的组合办法的趋同性,但这种组合可能带有负值。当这些方程式出现在所有$/R美元上时,我们显示我们的计划是非负内核的趋同。由于非本地的Neumann边界条件导致与无边框情况相同的配方,我们显示这些最后的结果也适用于Neumann问题。