Approximating Heavy-Tailed Distributions with a Mixture of Bernstein Phase-Type and Hyperexponential Models

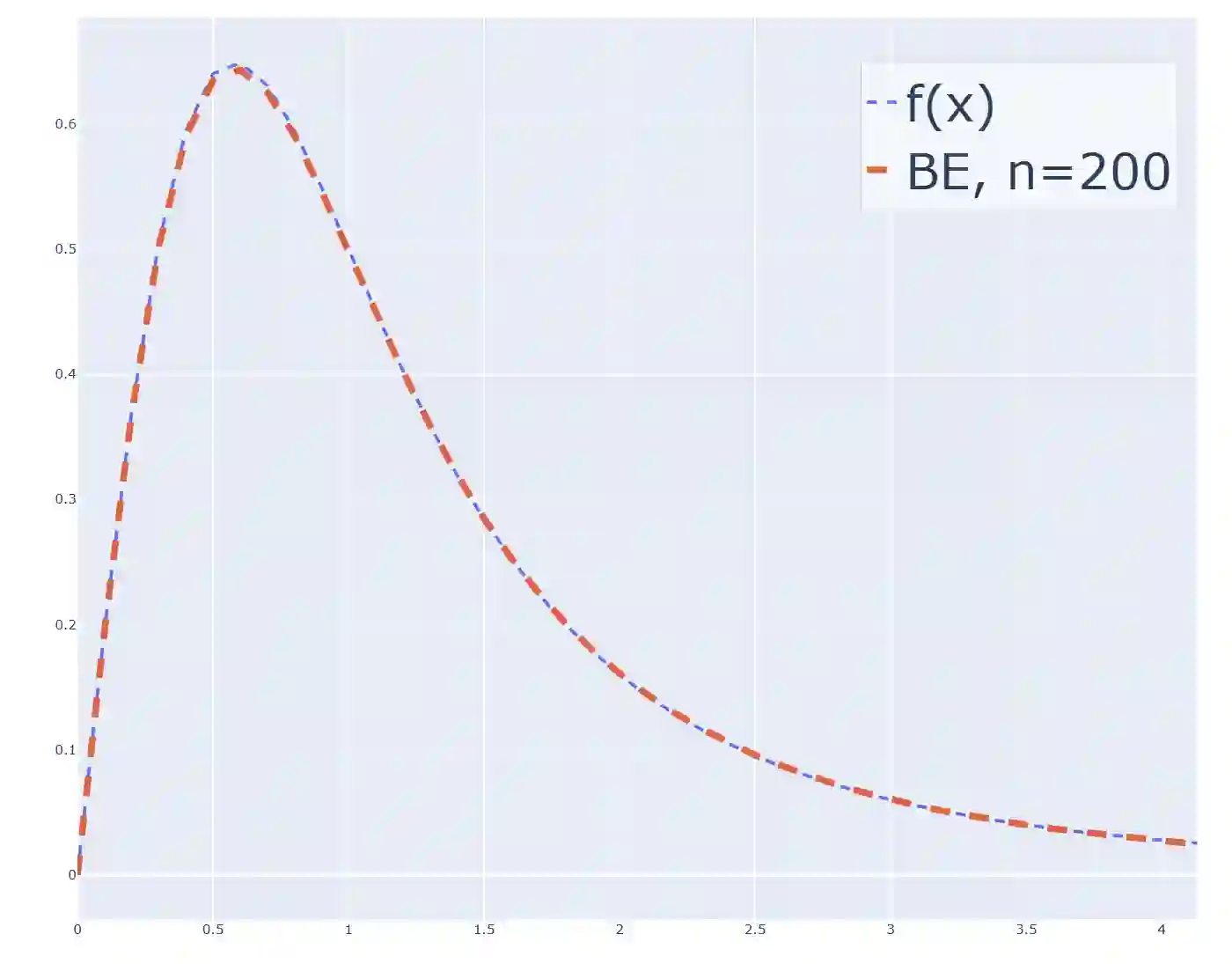
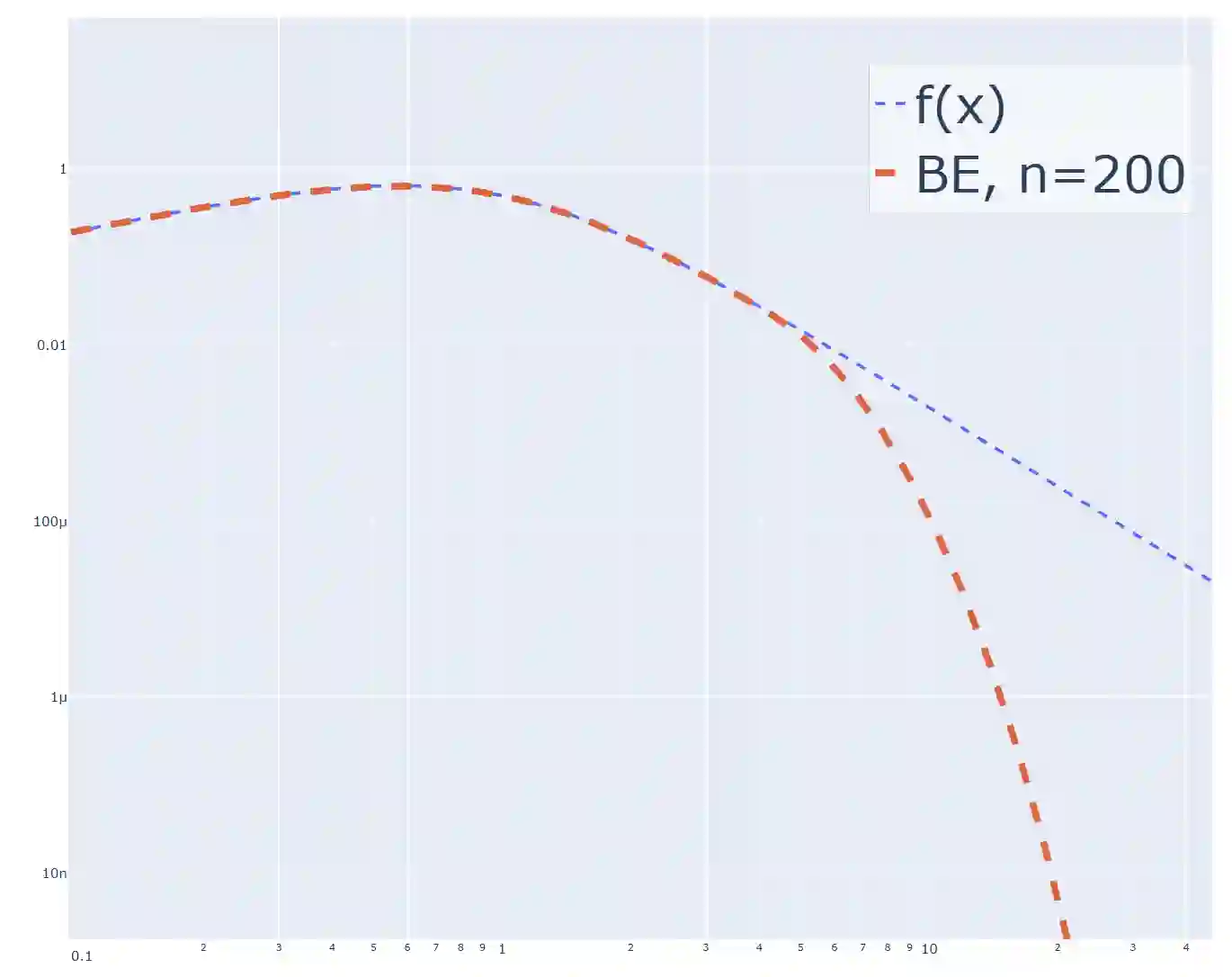
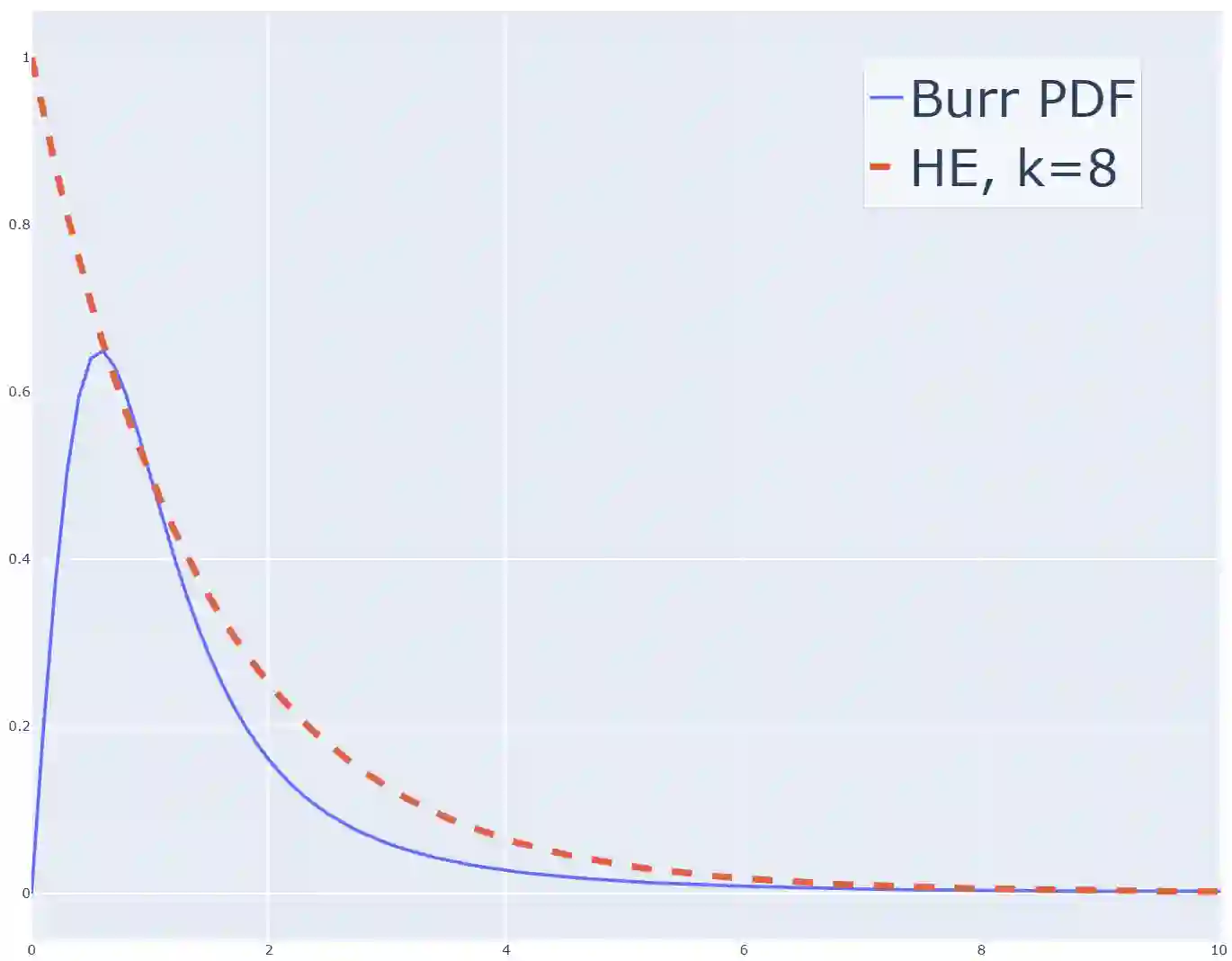
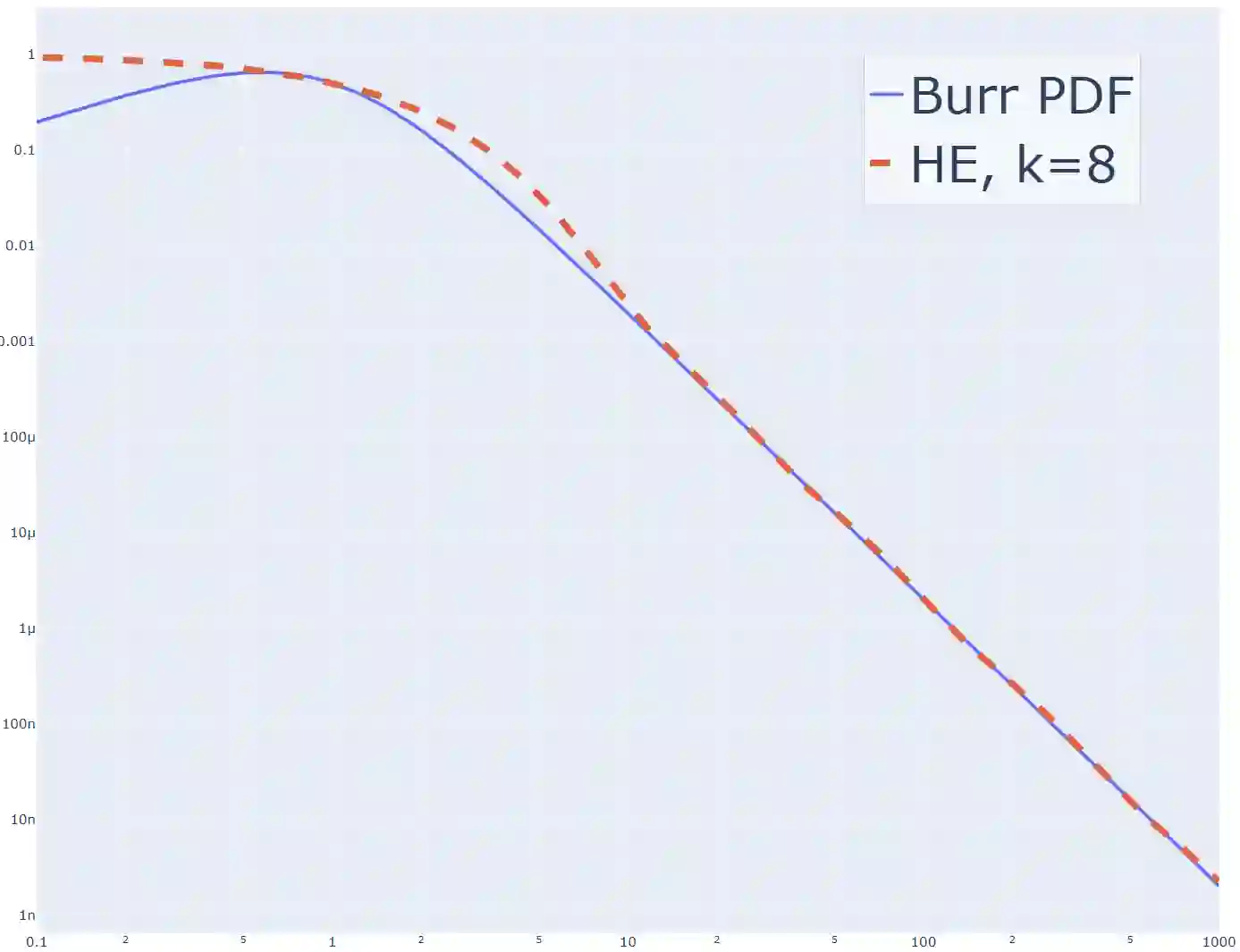
Heavy-tailed distributions, prevalent in a lot of real-world applications such as finance, telecommunications, queuing theory, and natural language processing, are challenging to model accurately owing to their slow tail decay. Bernstein phase-type (BPH) distributions, through their analytical tractability and good approximations in the non-tail region, can present a good solution, but they suffer from an inability to reproduce these heavy-tailed behaviors exactly, thus leading to inadequate performance in important tail areas. On the contrary, while highly adaptable to heavy-tailed distributions, hyperexponential (HE) models struggle in the body part of the distribution. Additionally, they are highly sensitive to initial parameter selection, significantly affecting their precision. To solve these issues, we propose a novel hybrid model of BPH and HE distributions, borrowing the most desirable features from each for enhanced approximation quality. Specifically, we leverage an optimization to set initial parameters for the HE component, significantly enhancing its robustness and reducing the possibility that the associated procedure results in an invalid HE model. Experimental validation demonstrates that the novel hybrid approach is more performant than individual application of BPH or HE models. More precisely, it can capture both the body and the tail of heavy-tailed distributions, with a considerable enhancement in matching parameters such as mean and coefficient of variation. Additional validation through experiments utilizing queuing theory proves the practical usefulness, accuracy, and precision of our hybrid approach.