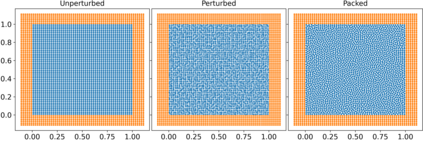
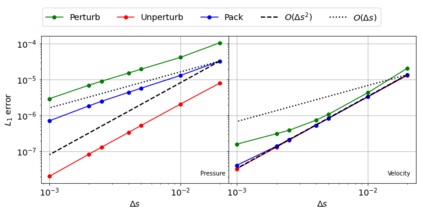
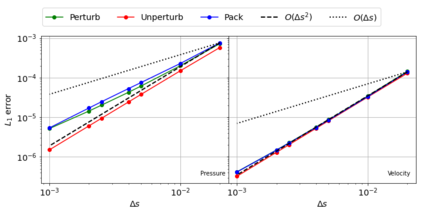
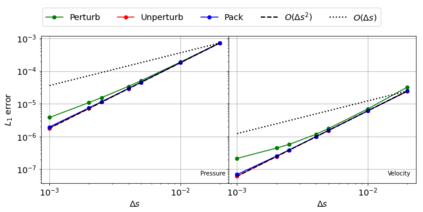
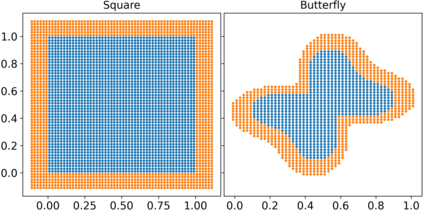
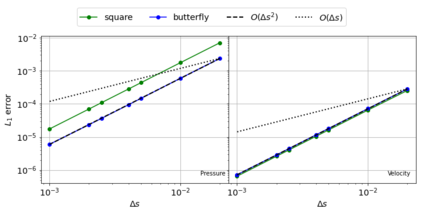
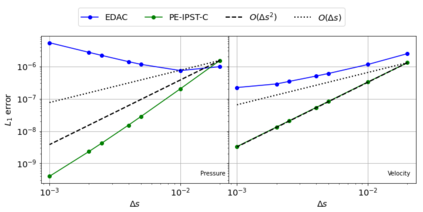
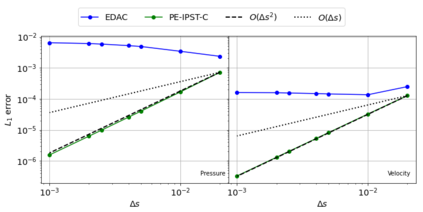
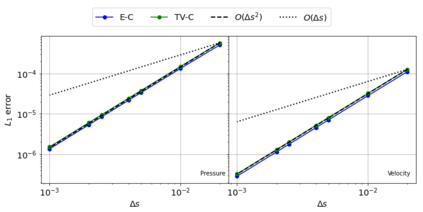
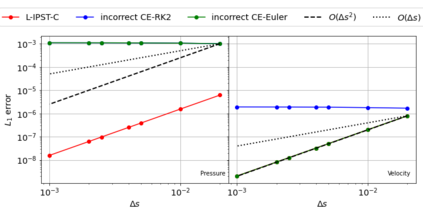
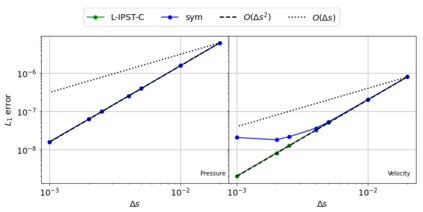
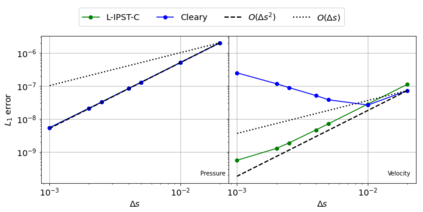
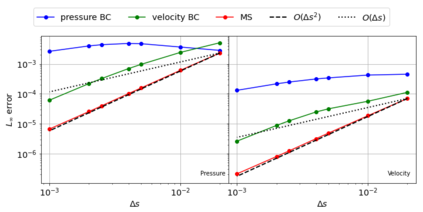
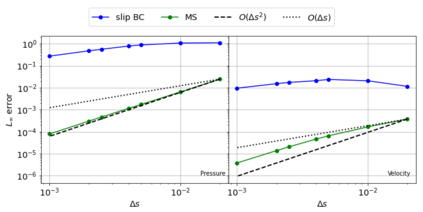
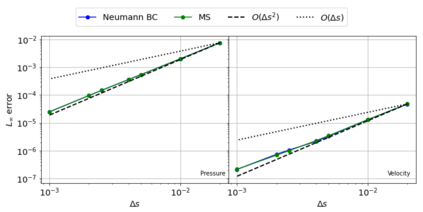
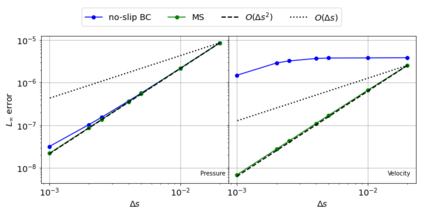
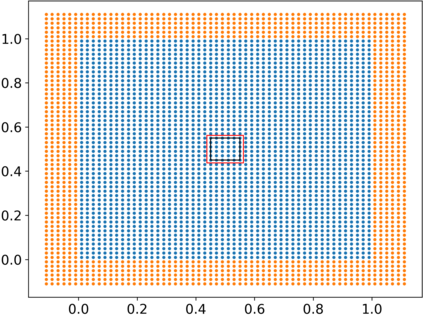
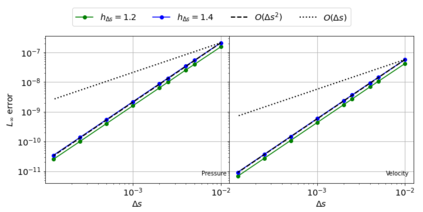
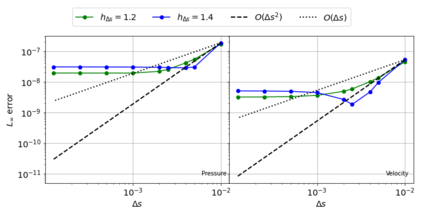
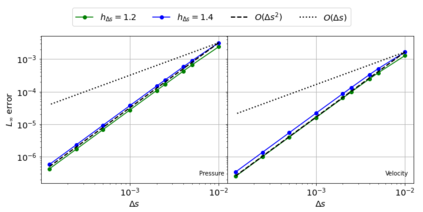
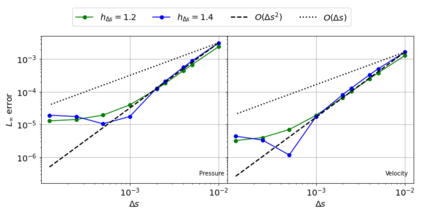
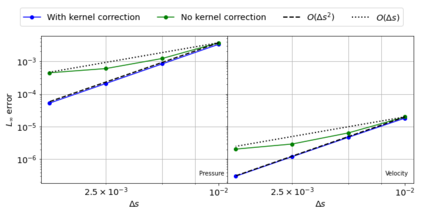
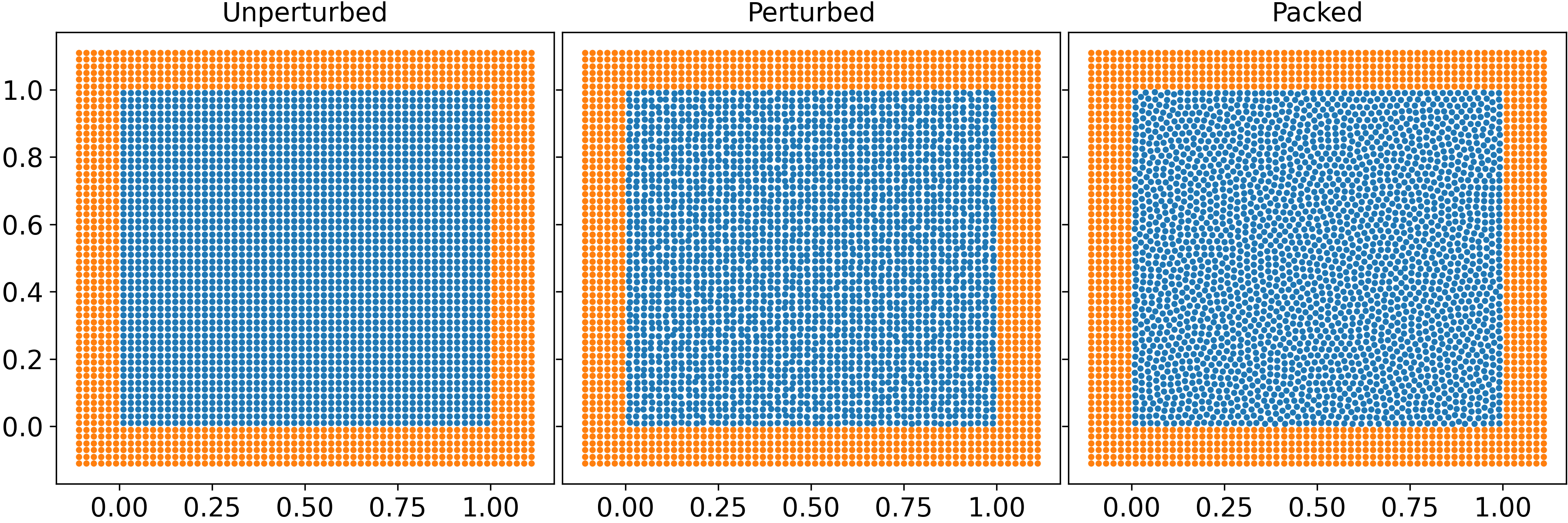
The Weakly-Compressible Smoothed Particle Hydrodynamics (WCSPH) method is a Lagrangian method that is typically used for the simulation of incompressible fluids. While developing an SPH-based scheme or solver, researchers often verify their code with exact solutions, solutions from other numerical techniques, or experimental data. This typically requires a significant amount of computational effort and does not test the full capabilities of the solver. Furthermore, often this does not yield insights on the convergence of the solver. In this paper we introduce the method of manufactured solutions (MMS) to comprehensively test a WCSPH-based solver in a robust and efficient manner. The MMS is well established in the context of mesh-based numerical solvers. We show how the method can be applied in the context of Lagrangian WCSPH solvers to test the convergence and accuracy of the solver in two and three dimensions, systematically identify any problems with the solver, and test the boundary conditions in an efficient way. We demonstrate this for both a traditional WCSPH scheme as well as for some recently proposed second order convergent WCSPH schemes. Our code is open source and the results of the manuscript are reproducible.
翻译:低压平流动粒子流体(WCSPH)方法是一种拉格朗格方法,通常用于模拟压压性液体。在开发以SPH为基础的办法或解答器时,研究人员往往用精确的解决方案、其他数字技术的解决方案或实验数据来核查其代码。这通常需要大量的计算努力,并且不测试解答器的全部能力。此外,这往往不会产生关于解答器汇合的洞察力。在本文中,我们引入了以稳健和有效的方式全面测试以WCSPH为基础的解决办法的制造方法。MMS在以网状为基础的数字解答器中已经牢固确立。我们展示了该方法如何在Lagrangian WCSPH解答器中应用,以两个和三个方面测试解答器的趋同和准确性,系统识别求解器的任何问题,并以有效的方式测试边界条件。我们用这个方法对传统的WCSPHPHS方案进行综合测试。对于最近提出的某些二级解析器来说,我们的代码是开放源结果。