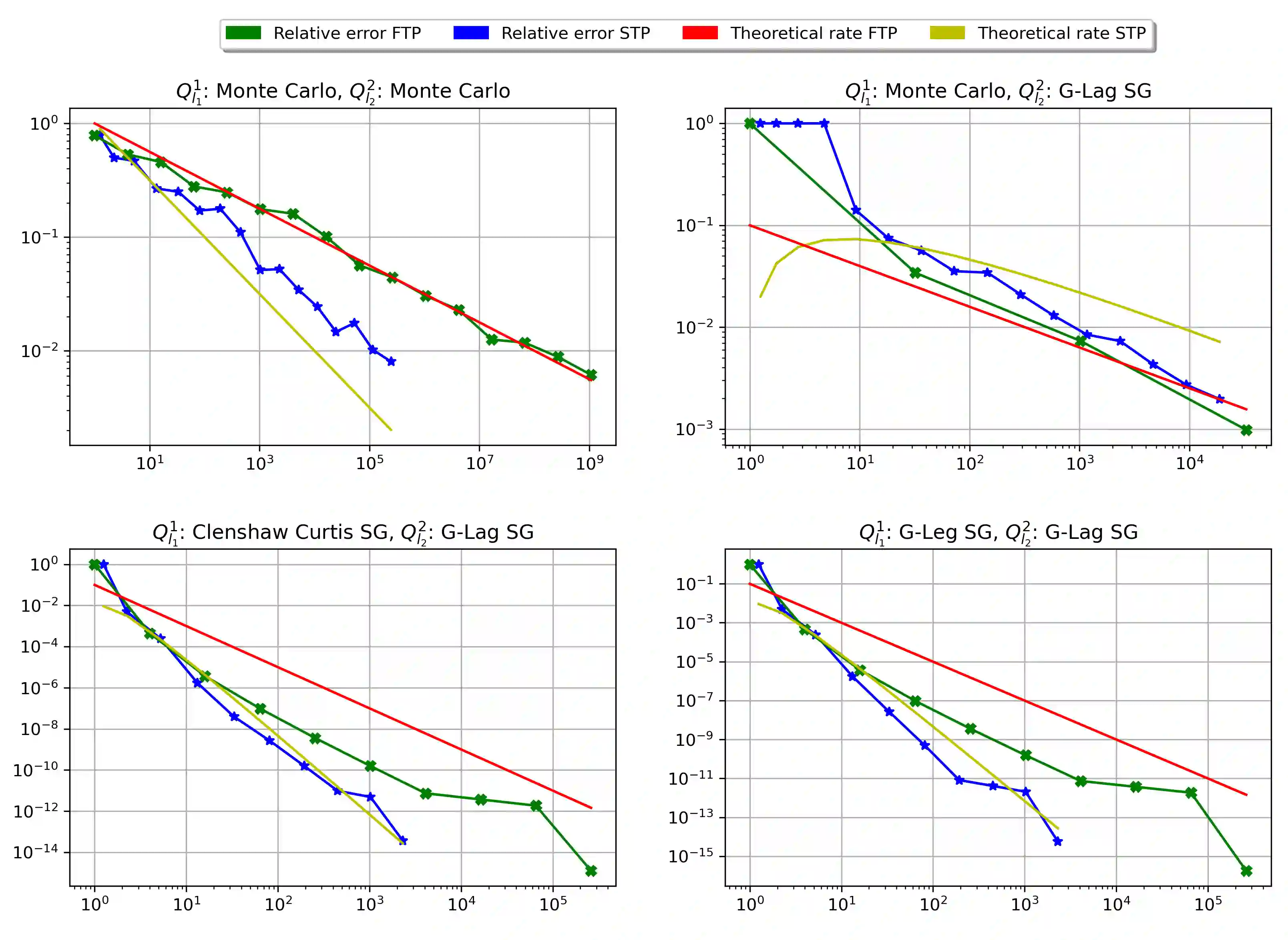
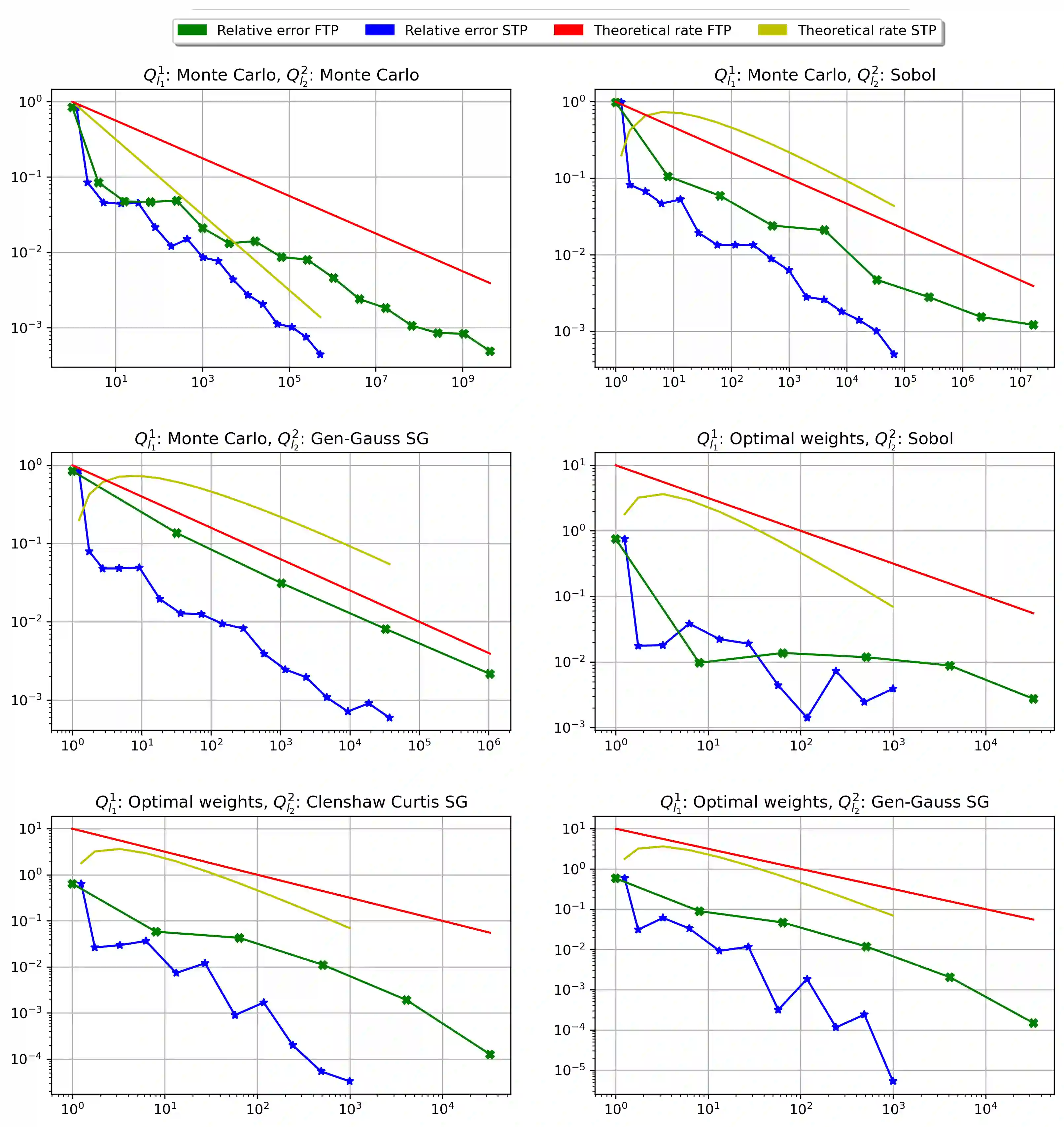
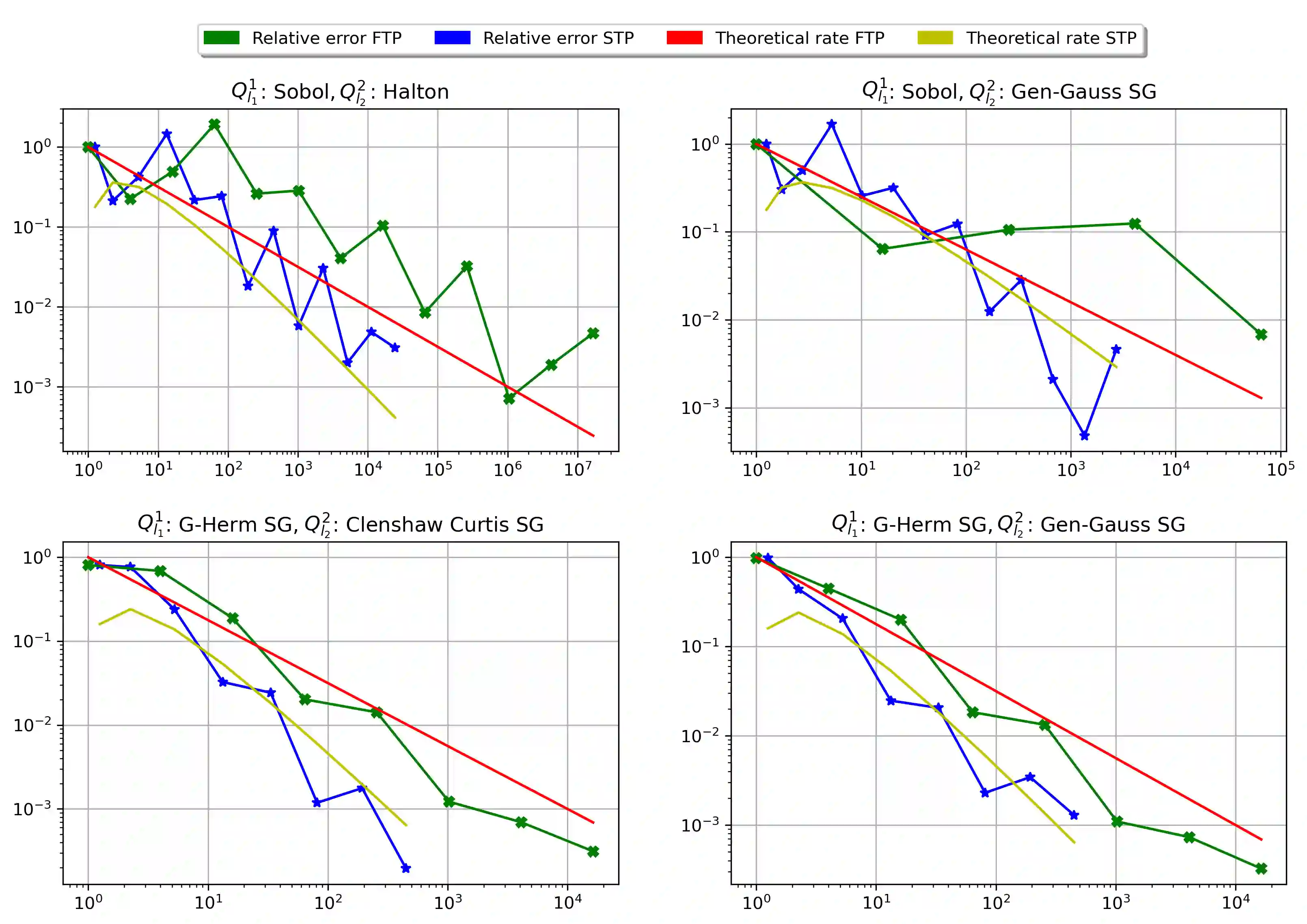
Generalized Method of Moments (GMM) estimators in their various forms, including the popular Maximum Likelihood (ML) estimator, are frequently applied for the evaluation of complex econometric models with not analytically computable moment or likelihood functions. As the objective functions of GMM- and ML-estimators themselves constitute the approximation of an integral, more precisely of the expected value over the real world data space, the question arises whether the approximation of the moment function and the simulation of the entire objective function can be combined. Motivated by the popular Probit and Mixed Logit models, we consider double integrals with a linking function which stems from the considered estimator, e.g. the logarithm for Maximum Likelihood, and apply a sparse tensor product quadrature to reduce the computational effort for the approximation of the combined integral. Given H\"older continuity of the linking function, we prove that this approach can improve the order of the convergence rate of the classical GMM- and ML-estimator by a factor of two, even for integrands of low regularity or high dimensionality. This result is illustrated by numerical simulations of Mixed Logit and Multinomial Probit integrals which are estimated by ML- and GMM-estimators, respectively.
翻译:由于GMM和ML估计结果的客观功能本身构成对真实世界数据空间的预期值的整体、更精确的近似值的近似值,因此产生了这样一个问题,即是否可将瞬时函数的近似值和整个目标功能的模拟值结合起来。在流行的Probit和混合逻辑模型的激励下,我们考虑双倍的组合值与从深思熟虑的估测器(例如,最大相似度的对数)产生的连接功能,并采用稀疏的加热值产品四边形来减少组合组合的计算努力。鉴于链接功能的H\"老的连续性,我们证明这一方法可以改善经典的GMM-和ML-估计结果的汇合率的顺序,以两个因素为动力,即使对于低定度的测算器(例如,最大相似度的对最大相似度的对数)和概率的对链接功能,我们也会考虑双重的结合功能,例如,并采用稀少的加的加的制产方方方方方形方形方形方形方形的测算结果,通过多度和高维的模拟分别以数字和高度测算的模拟显示的MMMMMM-M-MM-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-M-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I-I