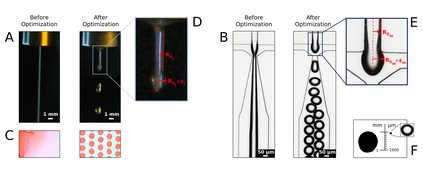
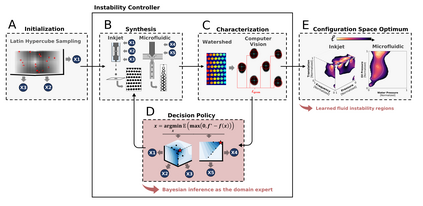
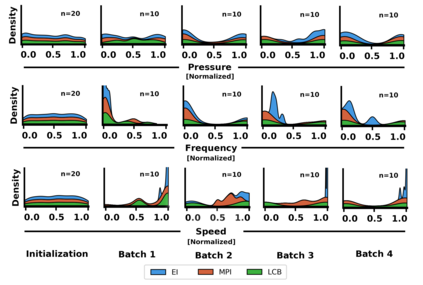
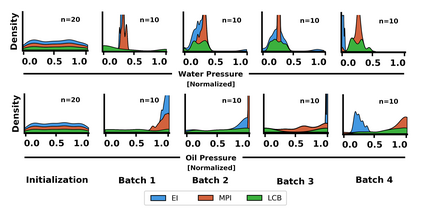
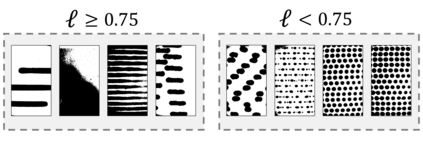
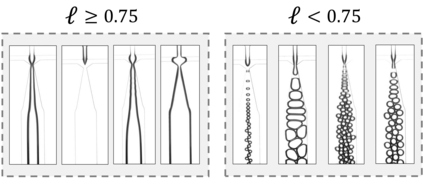
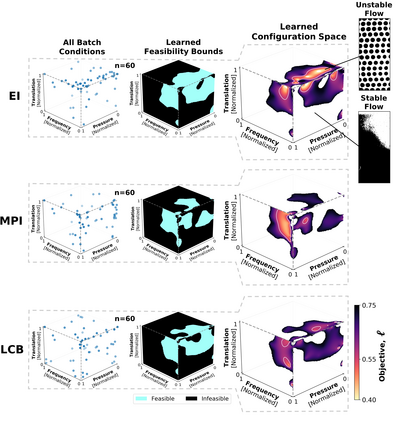
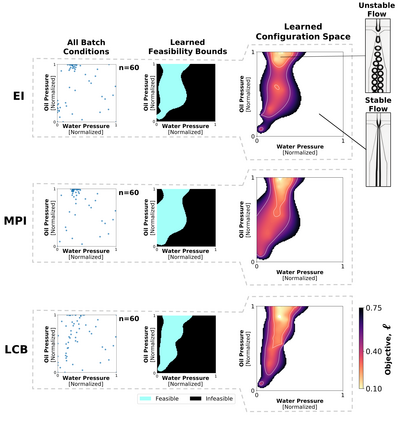
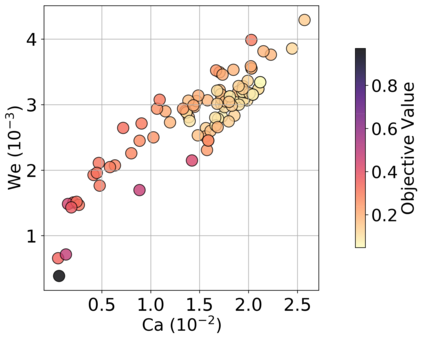
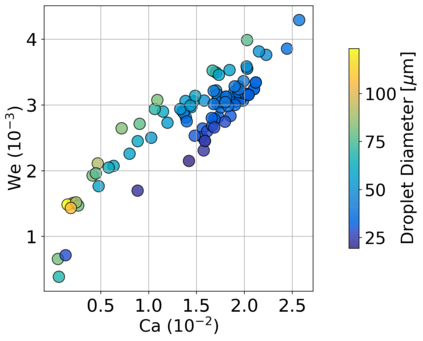
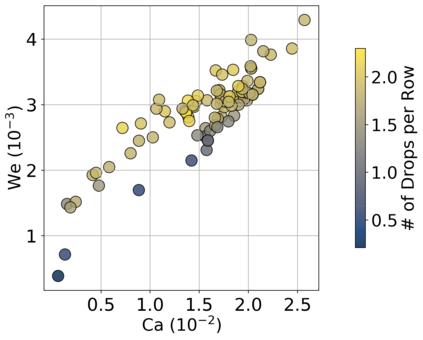
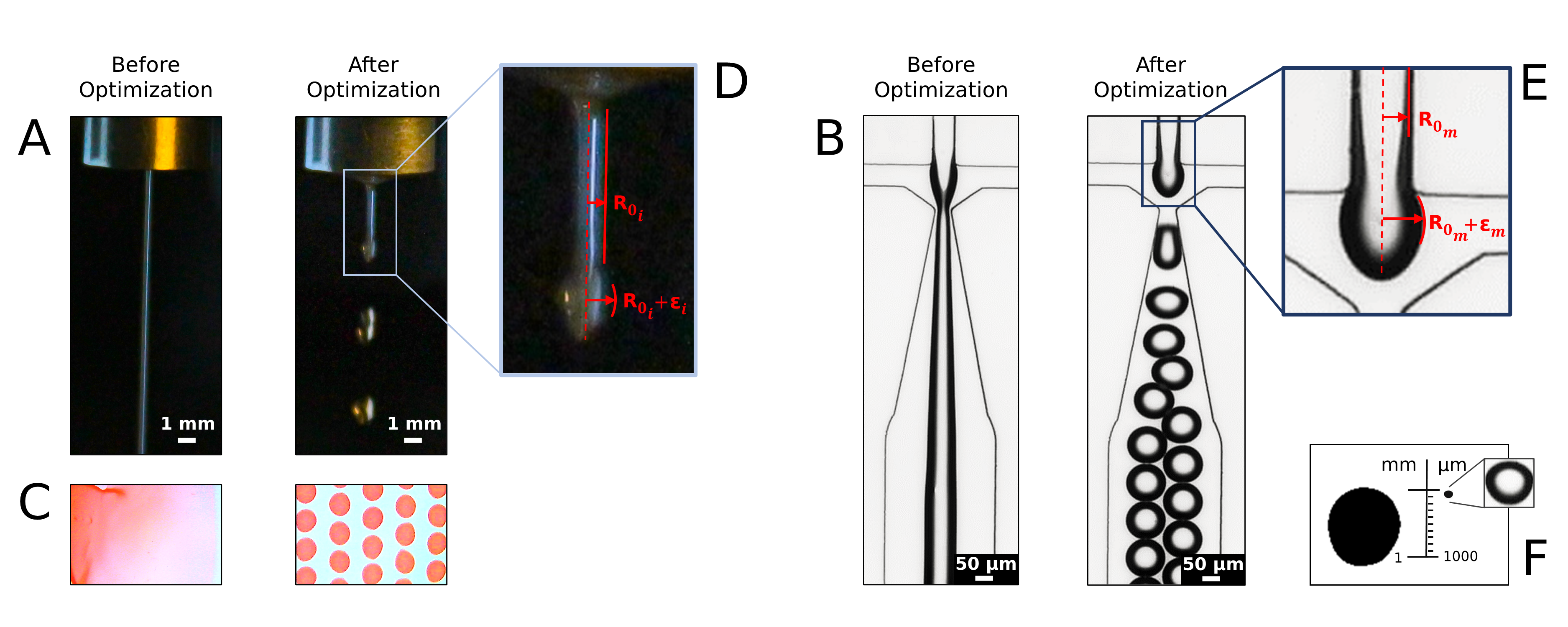
Autonomous optimization is a process by which hardware conditions are discovered that generate an optimized experimental product without the guidance of a domain expert. We design an autonomous optimization framework to discover the experimental conditions within fluid systems that generate discrete and uniform droplet patterns. Generating discrete and uniform droplets requires high-precision control over the experimental conditions of a fluid system. Fluid stream instabilities, such as Rayleigh-Plateau instability and capillary instability, drive the separation of a flow into individual droplets. However, because this phenomenon leverages an instability, by nature the hardware must be precisely tuned to achieve uniform, repeatable droplets. Typically this requires a domain expert in the loop and constant re-tuning depending on the hardware configuration and liquid precursor selection. Herein, we propose a computer vision-driven Bayesian optimization framework to discover the precise hardware conditions that generate uniform, reproducible droplets with the desired features, leveraging flow instability without a domain expert in the loop. This framework is validated on two fluid systems, at the micrometer and millimeter length scales, using microfluidic and inkjet systems, respectively, indicating the application breadth of this approach.
翻译:自动优化是一个过程,通过它发现硬件条件,在没有域专家的指导下产生最佳实验产品; 我们设计一个自主优化框架,以发现流体系统中产生离散和统一的滴子模式的实验条件; 产生离散和统一的滴子,要求对流体的实验条件进行高精度控制; 流体流不稳定,如Raylei-Plateau不稳定和毛细不稳,驱动流体流向单个滴子的分离。 然而,由于这种现象造成不稳定,因此,从性质上来说,硬件必须精确调整,以达到统一和可重复的滴子。 通常这需要根据硬件配置和液体前体选择,在循环和不断调整方面有一名域专家。 在此,我们提出一个计算机驱动的巴耶斯优化框架,以发现产生统一、可复制的滴子及其预期特性的精确硬件条件,在没有循环的域专家的情况下利用流动不稳定。 这个框架在微米计和毫米长度尺度上对两个流体系统进行验证, 分别使用微氟化和内基喷射系统, 表明这一方法的应用范围。