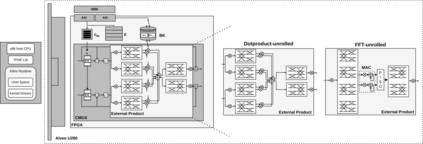
Fully Homomorphic Encryption is a technique that allows computation on encrypted data. It has the potential to drastically change privacy considerations in the cloud, but high computational and memory overheads are preventing its broad adoption. TFHE is a promising Torus-based FHE scheme that heavily relies on bootstrapping, the noise-removal tool that must be invoked after every encrypted gate computation. We present FPT, a Fixed-Point FPGA accelerator for TFHE bootstrapping. FPT is the first hardware accelerator to heavily exploit the inherent noise present in FHE calculations. Instead of double or single-precision floating-point arithmetic, it implements TFHE bootstrapping entirely with approximate fixed-point arithmetic. Using an in-depth analysis of noise propagation in bootstrapping FFT computations, FPT is able to use noise-trimmed fixed-point representations that are up to 50% smaller than prior implementations using floating-point or integer FFTs. FPT's microarchitecture is built as a streaming processor inspired by traditional streaming DSPs: it instantiates high-throughput computational stages that are directly cascaded, with simplified control logic and routing networks. FPT's streaming approach allows 100% utilization of arithmetic units and requires only small bootstrapping key caches, enabling an entirely compute-bound bootstrapping throughput of 1 BS / 35$\mu$s. This is in stark contrast to the established classical CPU approach to FHE bootstrapping acceleration, which tends to be heavily memory and bandwidth-constrained. FPT is fully implemented and evaluated as a bootstrapping FPGA kernel for an Alveo U280 datacenter accelerator card. FPT achieves almost three orders of magnitude higher bootstrapping throughput than existing CPU-based implementations, and 2.5$\times$ higher throughput compared to recent ASIC emulation experiments.
翻译:完全基因加密是一种允许计算加密数据的技术。 它有可能大幅改变云层中的隐私考虑, 但高计算和存储管理令阻止其广泛采用。 TFHE 是一个充满希望的托鲁斯基FHE计划, 在很大程度上依赖靴子安装, 每次加密门运算后必须使用清除噪音的工具。 我们提供了固定点 FPT, 用于TFHE 的固定点 FPGA 加速器。 FPT 是第一个大量利用 FHE 计算中固有的加速度的硬件加速器。 而不是双或单精度浮动浮点计算, 而是用近似固定点的算术来实施。 TFHE 执行中, 使用音调固定点的固定点显示器。 FPT( PFGA) 。 FPT 的微缩缩缩缩缩缩图比传统流 DSP 的流动进程要快得多。 它使用直流式的直流式螺旋路路路路路路路35号, 正在直接操作的FPTFPTFPD 版本操作系统操作系统运行中, 需要一个最近的快速化的平流化的直流控制。