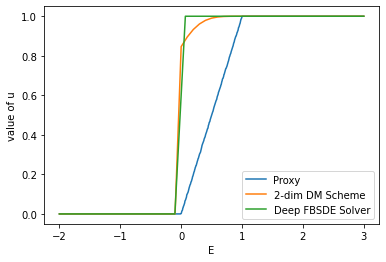
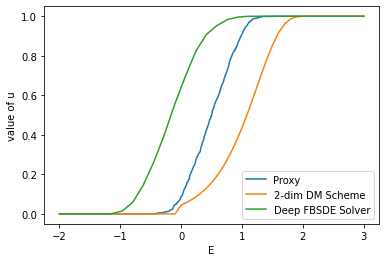
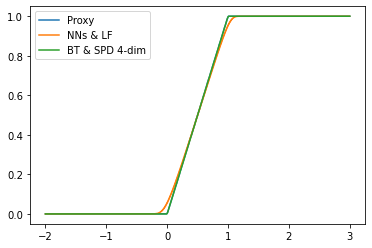
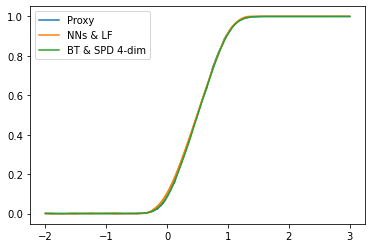
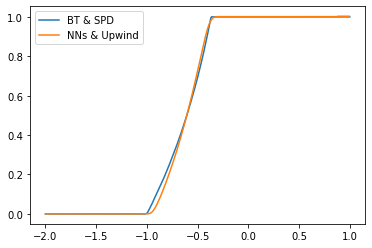
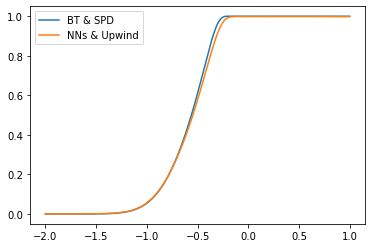
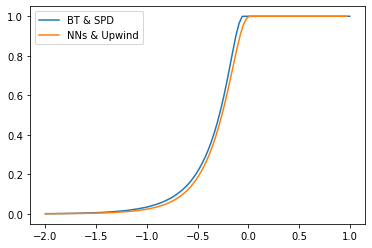
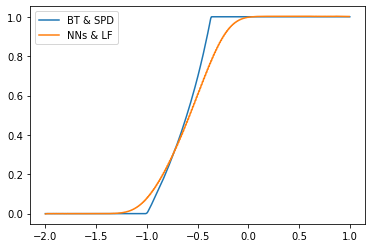
In this work, we study the numerical approximation of a class of singular fully coupled forward backward stochastic differential equations. These equations have a degenerate forward component and non-smooth terminal condition. They are used, for example, in the modeling of carbon market[9] and are linked to scalar conservation law perturbed by a diffusion. Classical FBSDEs methods fail to capture the correct entropy solution to the associated quasi-linear PDE. We introduce a splitting approach that circumvent this difficulty by treating differently the numerical approximation of the diffusion part and the non-linear transport part. Under the structural condition guaranteeing the well-posedness of the singular FBSDEs [8], we show that the splitting method is convergent with a rate $1/2$. We implement the splitting scheme combining non-linear regression based on deep neural networks and conservative finite difference schemes. The numerical tests show very good results in possibly high dimensional framework.
翻译:在这项工作中,我们研究一个完全相联的单单类完全前向后向随机差异方程式的数值近似值。这些方程式具有退化的前方元件和非偏向终端条件。例如,在碳市场模型[9] 中,它们被使用,并被扩散所侵扰的星际保护法所链接。经典FBSDEs方法未能为相关的准线性PDE找到正确的诱变方程式。我们引入了一种分解方法,通过区别对待扩散部分和非线性运输部分的数字近似值来绕过这一困难。在保证单一FBSDEs稳健可靠的结构条件[8]下,我们显示分裂法与1/2美元的汇率相融合。我们实施了基于深线性网络和保守的有限差异方案的非线性回归分解法。数字测试在可能的高维度框架中显示了非常好的结果。