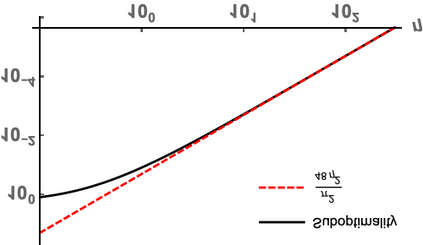
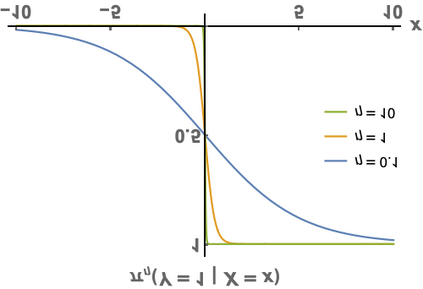
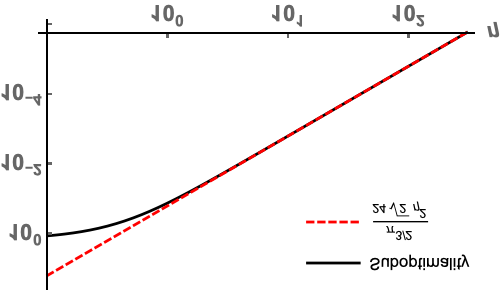
We compute exact second-order asymptotics for the cost of an optimal solution to the entropic optimal transport problem in the continuous-to-discrete, or semi-discrete, setting. In contrast to the discrete-discrete or continuous-continuous case, we show that the first-order term in this expansion vanishes but the second-order term does not, so that in the semi-discrete setting the difference in cost between the unregularized and regularized solution is quadratic in the inverse regularization parameter, with a leading constant that depends explicitly on the value of the density at the points of discontinuity of the optimal unregularized map between the measures. We develop these results by proving new pointwise convergence rates of the solutions to the dual problem, which may be of independent interest.
翻译:在连续到分解或半分解的设置中,我们计算出最佳运输问题最佳最佳解决办法的成本,精确的第二顺序假设。与离散、分解或连续的情况相反,我们表明,这一扩展的一阶术语消失了,但第二阶术语没有消失,因此,在确定非常规和正规化解决办法之间成本差异的半分界线参数中,在反向正规化参数中,四角变量是一个主要常数,明确取决于在措施之间最佳非正规化地图中断点的密度值。我们通过证明对可能具有独立利益的双重问题的解决办法的新点性趋同率来发展这些结果。