Consistent coupling of positions and rotations for embedding 1D Cosserat beams into 3D solid volumes

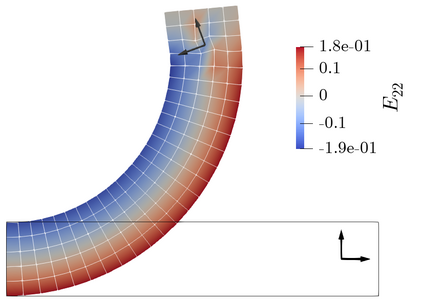
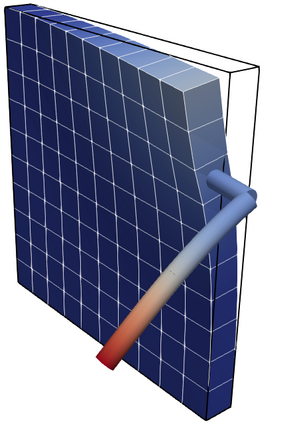
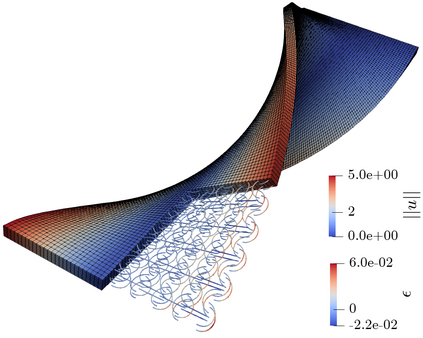
This article proposes a mortar type finite element formulation for consistently embedding curved, slender beams, i.e. 1D Cosserat continua, into 3D solid volumes. A consistent 1D-3D coupling scheme for this problem type is proposed, which enforces both positional and rotational constraints. Since Boltzmann continua exhibit no inherent rotational degrees of freedom, suitable definitions of orthonormal triads are investigated that are representative for the orientation of material directions in the 3D solid. The rotation tensor defined by the polar decomposition of the deformation gradient is demonstrated to represent these material directions in a L2-optimal manner. Subsequently, objective rotational coupling constraints between beam and solid are formulated and enforced in a variationally consistent framework. Eventually, finite element discretization of all primary fields results in an embedded mortar formulation for rotational and translational constraint enforcement. Based on carefully chosen numerical test cases, the proposed scheme is demonstrated to exhibit a consistent spatial convergence behavior and to offer the up-scaling potential for studying real-life engineering applications such as fiber-reinforced composite materials.