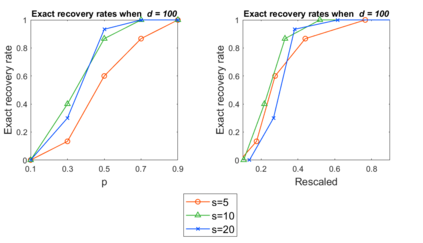
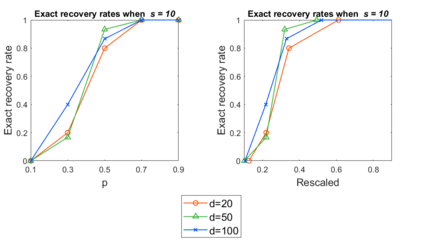
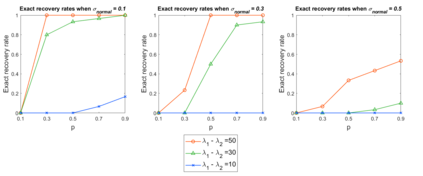
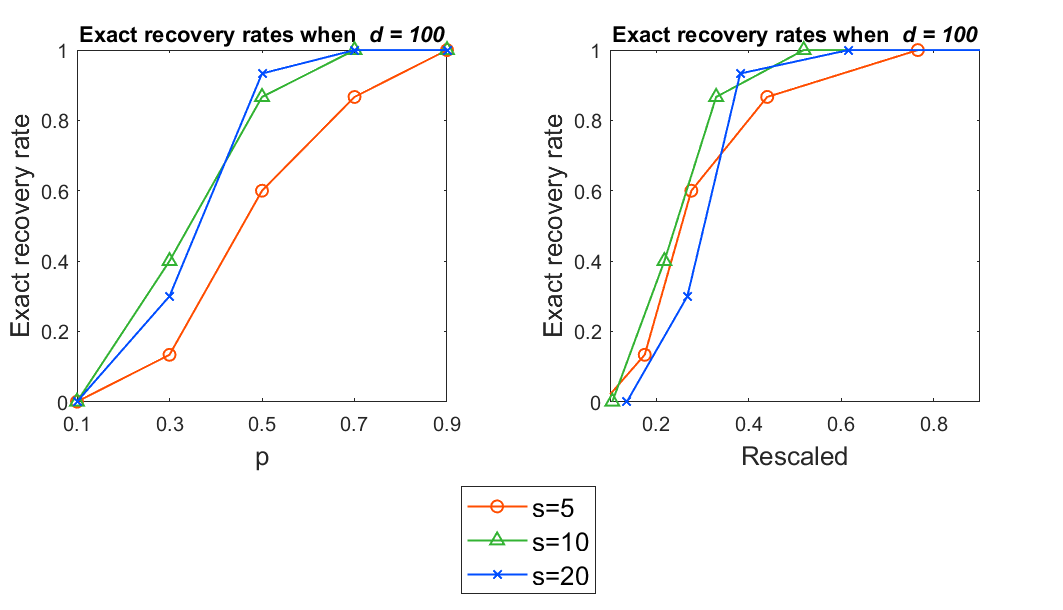
We study a practical algorithm for sparse principal component analysis (PCA) of incomplete and noisy data. Our algorithm is based on the semidefinite program (SDP) relaxation of the non-convex $l_1$-regularized PCA problem. We provide theoretical and experimental evidence that SDP enables us to exactly recover the true support of the sparse leading eigenvector of the unknown true matrix, despite only observing an incomplete (missing uniformly at random) and noisy version of it. We derive sufficient conditions for exact recovery, which involve matrix incoherence, the spectral gap between the largest and second-largest eigenvalues, the observation probability and the noise variance. We validate our theoretical results with incomplete synthetic data, and show encouraging and meaningful results on a gene expression dataset.
翻译:我们研究一种实用的算法,用于对不完整和吵闹的数据进行稀少的主要组成部分分析(PCA),我们的算法基于非convex $l_1$1美元正规化的五氯苯问题的半确定性程序(SDP)松散。我们提供了理论和实验证据,证明SDP使我们能够完全恢复未知真实矩阵的稀疏主要原始人的真正支持,尽管我们只观察到一个不完整(随机地一致)和杂乱的版本。我们为精确的恢复创造了充分的条件,这涉及到矩阵不一致性、最大和第二大电子值之间的光谱差距、观测概率和噪音差异。我们用不完整的合成数据来验证我们的理论结果,并显示基因表达数据集的令人鼓舞的和有意义的结果。