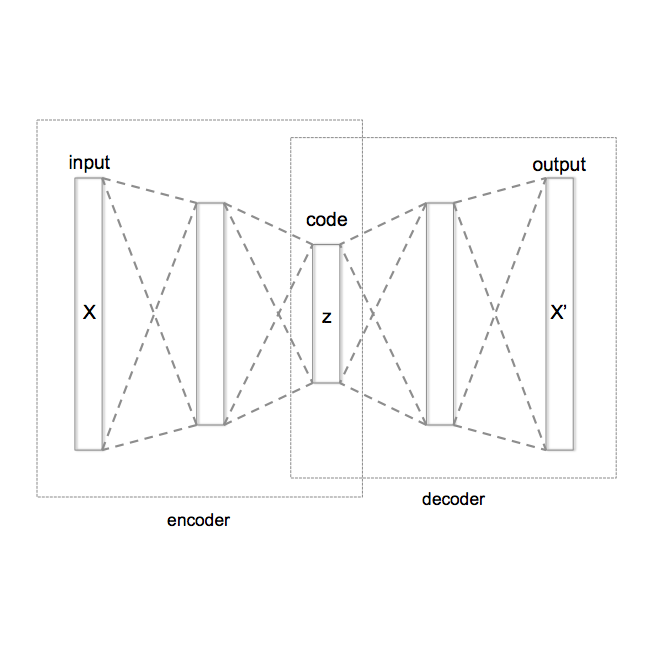
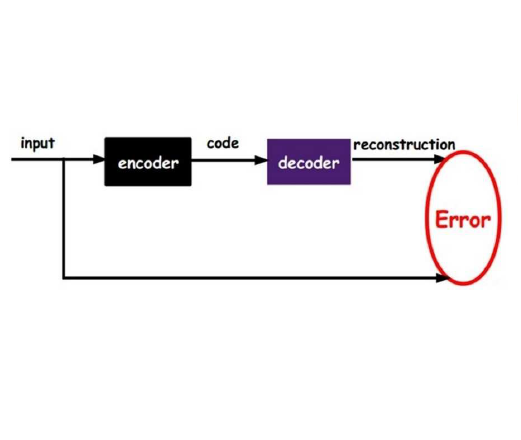
Among other uses, neural networks are a powerful tool for solving deterministic and Bayesian inverse problems in real-time. In the Bayesian framework, variational autoencoders, a specialized type of neural network, enable the estimation of model parameters and their distribution based on observational data allowing to perform real-time inverse uncertainty quantification. In this work, we build upon existing research [Goh, H. et al., Proceedings of Machine Learning Research, 2022] by proposing a novel loss function to train variational autoencoders for Bayesian inverse problems. When the forward map is affine, we provide a theoretical proof of the convergence of the latent states of variational autoencoders to the posterior distribution of the model parameters. We validate this theoretical result through numerical tests and we compare the proposed variational autoencoder with the existing one in the literature. Finally, we test the proposed variational autoencoder on the Laplace equation.
翻译:暂无翻译