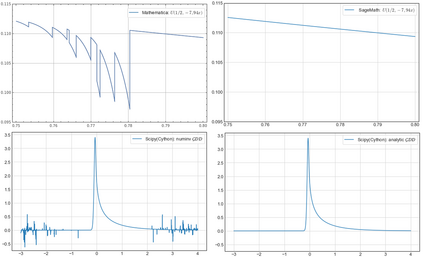
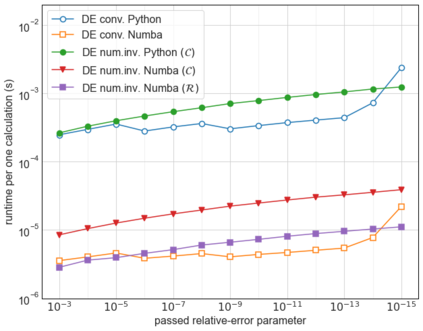
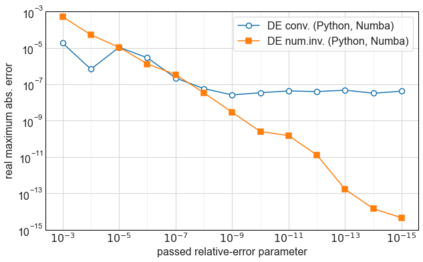
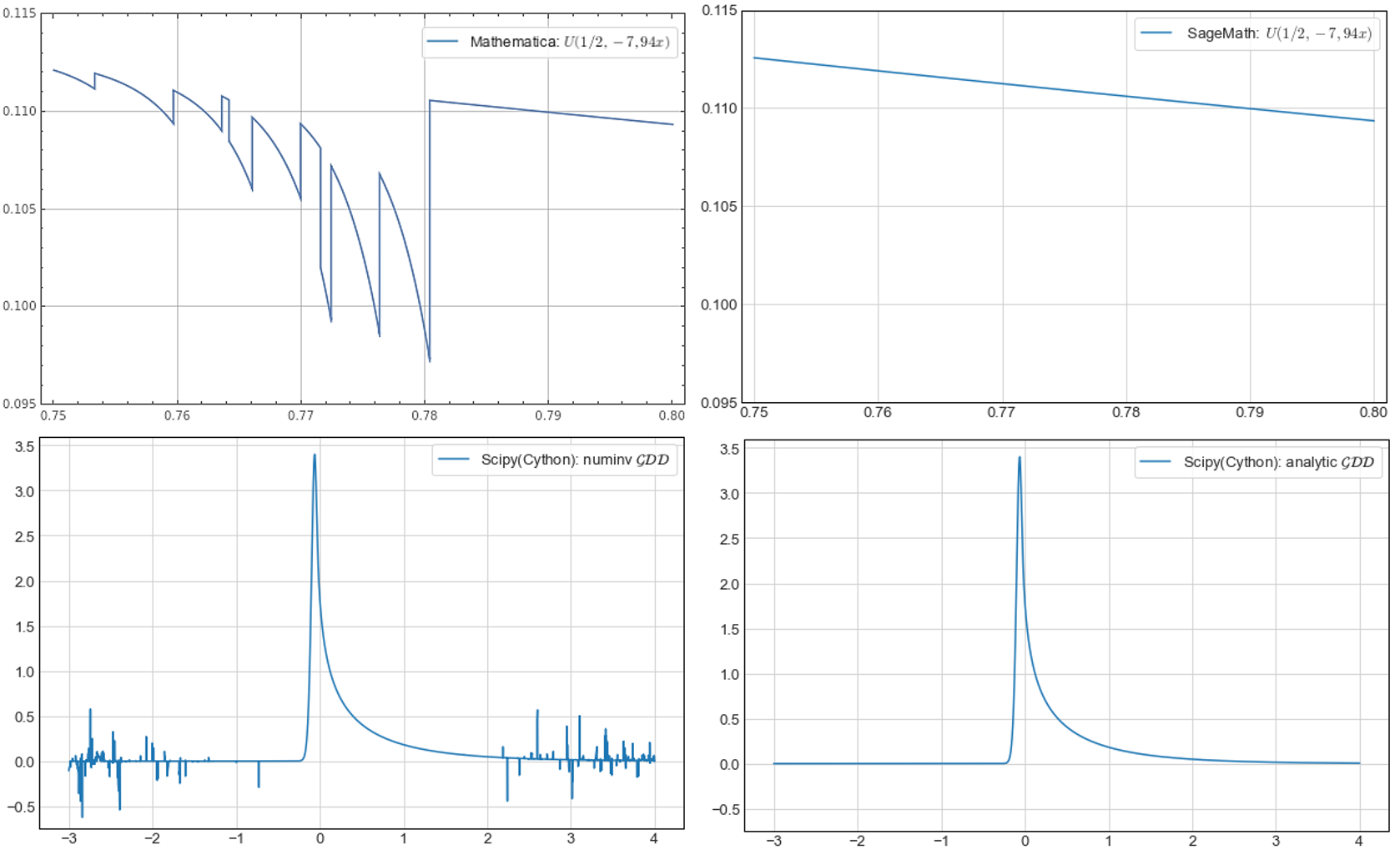
At present, there is still no officially accepted and extensively verified implementation of computing the gamma difference distribution allowing unequal shape parameters. We explore four computational ways of the gamma difference distribution with the different shape parameters resulting from time series kriging, a forecasting approach based on the best linear unbiased prediction, and linear mixed models. The results of our numerical study, with emphasis on using open data science tools, demonstrate that our open tool implemented in high-performance Python(with Numba) is exponentially fast, highly accurate, and very reliable. It combines numerical inversion of the characteristic function and the trapezoidal rule with the double exponential oscillatory transformation (DE quadrature). At the double 53-bit precision, our tool outperformed the speed of the analytical computation based on Tricomi's $U(a, b, z)$ function in CAS software (commercial Mathematica, open SageMath) by 1.5-2 orders. At the precision of scientific numerical computational tools, it exceeded open SciPy, NumPy, and commercial MATLAB 5-10 times. The potential future application of our tool for a mixture of characteristic functions could open new possibilities for fast data analysis based on exact probability distributions in areas like multidimensional statistics, measurement uncertainty analysis in metrology as well as in financial mathematics and risk analysis.
翻译:目前,在计算伽马差异分布时,仍然没有正式接受和广泛核实的计算伽马差异分布方法,并允许不均匀的形状参数。我们探索了四种伽马差异分布的计算方法,以及由时间序列Kriging产生的不同形状参数,一种基于最佳线性不偏预测的预测方法,以及线性混合模型。我们进行的数字研究的结果,重点是使用开放的数据科学工具,表明我们在高性能Python(与Numba一起)中实施的开放工具是指数快速、高度准确和非常可靠的。它将特性函数和捕捉性分裂规则的数字转换与双倍指数悬浮变异(DE sequadratural)结合起来。在53比精确度的两倍中,我们的工具超过了基于Tricomi's $U(a, b, z) 和线性混合模型的分析速度。我们的工具在CASAIS软件(商业数学、开放SageMatth)中以1.5-2顺序实施的开放工具,它超过了开放的SciPy、NumPy和商用MATLAB 5-10次的概率分析中的潜在工具,在快速数据分析中作为快速的概率分析领域,可以将我们的工具作为快速分析的概率的模型分析的模型的模型的模型的模型的模型中进行分配。