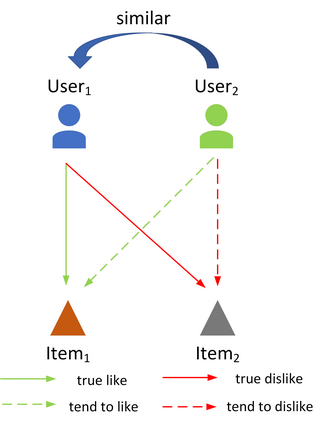
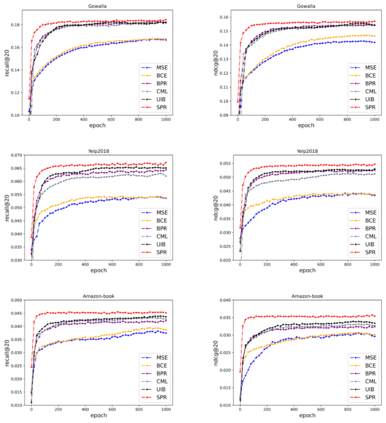
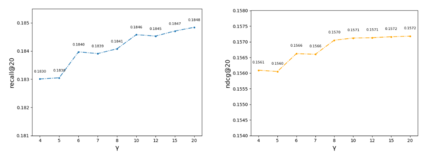
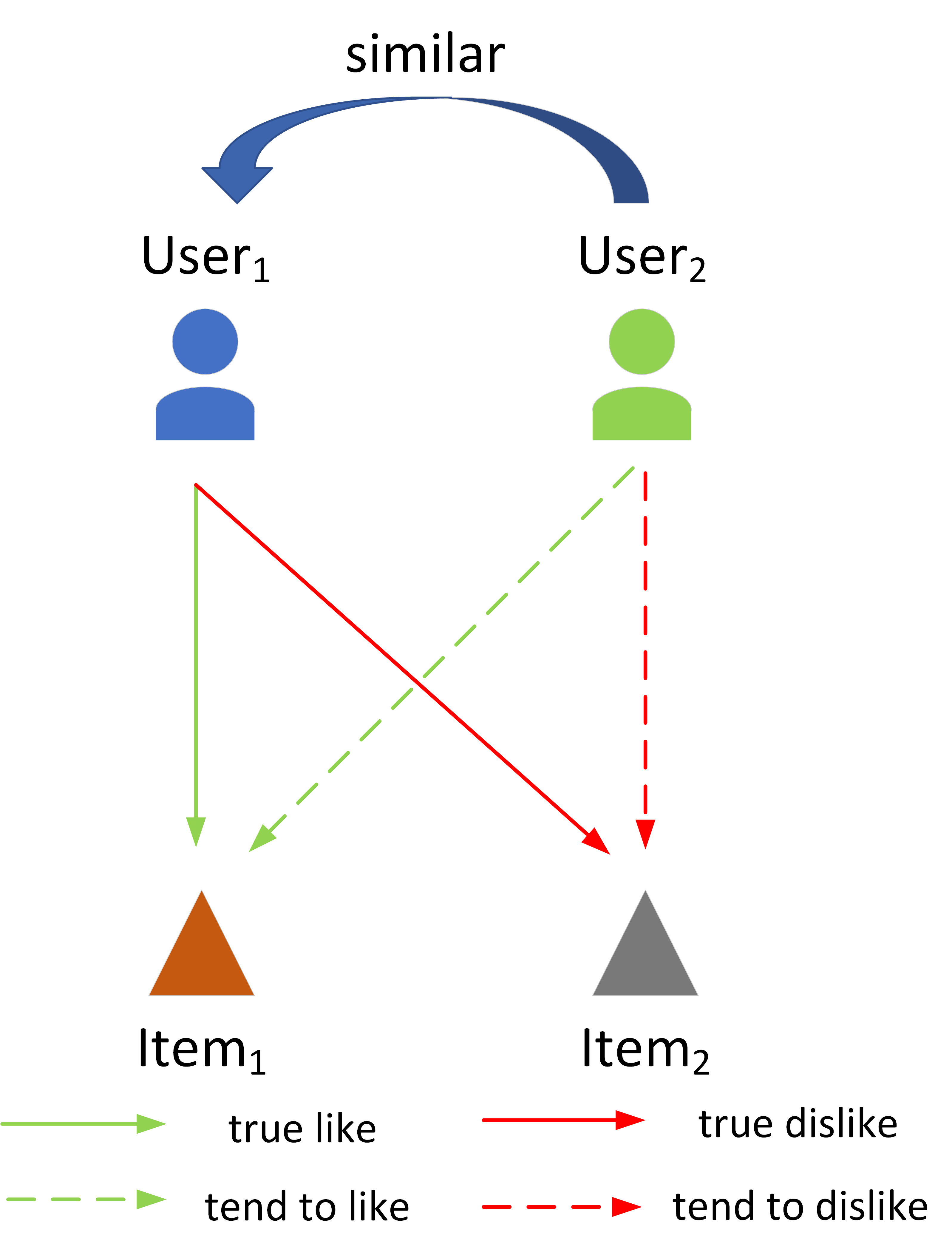
The goal of a recommendation system is to model the relevance between each user and each item through the user-item interaction history, so that maximize the positive samples score and minimize negative samples. Currently, two popular loss functions are widely used to optimize recommender systems: the pointwise and the pairwise. Although these loss functions are widely used, however, there are two problems. (1) These traditional loss functions do not fit the goals of recommendation systems adequately and utilize prior knowledge information sufficiently. (2) The slow convergence speed of these traditional loss functions makes the practical application of various recommendation models difficult. To address these issues, we propose a novel loss function named Supervised Personalized Ranking (SPR) Based on Prior Knowledge. The proposed method improves the BPR loss by exploiting the prior knowledge on the interaction history of each user or item in the raw data. Unlike BPR, instead of constructing <user, positive item, negative item> triples, the proposed SPR constructs <user, similar user, positive item, negative item> quadruples. Although SPR is very simple, it is very effective. Extensive experiments show that our proposed SPR not only achieves better recommendation performance, but also significantly accelerates the convergence speed, resulting in a significant reduction in the required training time.
翻译:建议系统的目标是通过用户-项目互动历史来模拟每个用户和每个项目之间的关联性,以便最大限度地实现正样样本评分,并尽量减少负样样本。目前,广泛使用两个受欢迎的损失功能来优化建议系统:点和对等。虽然这些损失功能被广泛使用,但有两个问题。 (1) 这些传统的损失功能不符合建议系统的目标,并充分利用了先前的知识信息。(2) 这些传统损失功能的趋同速度缓慢,使得各种建议模型难以实际应用。为解决这些问题,我们提议了一个名为 " 以先前知识为基础的个人化监督分级(SPR) " 的新的损失函数。拟议的方法通过利用以前关于每个用户或原始数据中项目互动历史的知识改进BPR损失。与BPR不同的是,SPR不是建造 < 用户、正项、负项、负项] 三倍,而拟议的SPR则构建了 < 用户、类似用户、正项、负项、负项] 的四分立。尽管SPR非常简单,但非常有效。广泛的实验表明,我们提议的SPR不仅能够大大缩短培训速度,而且还大大加快了进度。