Locality-sensitive bucketing functions

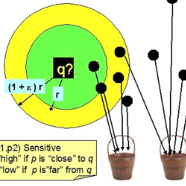
Many bioinformatics applications involve bucketing a set of sequences where each sequence is allowed to be assigned into multiple buckets. To achieve both high sensitivity and precision, bucketing methods are desired to assign similar sequences into the same buckets while assigning dissimilar sequences into distinct buckets. Existing $k$-mer-based bucketing methods have been efficient in processing sequencing data with low-error rate, but encounter much reduced sensitivity on data with high-error rate. Locality-sensitive hashing (LSH) schemes are able to mitigate this issue through tolerating the edits in similar sequences, but state-of-the-art methods still have large gap. Here we generalize the LSH function by allowing it to hash one sequence into multiple buckets. Formally, a bucketing function, which maps a sequence (of fixed length) into a subset of buckets, is defined to be $(d_1, d_2)$-sensitive if any two sequences within an edit distance of $d_1$ are mapped into at least one shared bucket, and any two sequences with distance at least $d_2$ are mapped into disjoint subsets of buckets. We construct LSB functions with a variety of values of $(d_1,d_2)$ and analyze their efficiency with respect to the total number of buckets needed as well as the number of buckets that a specific sequence is mapped to. We also prove lower bounds of these two parameters in different settings and show that some of our constructed LSB functions are optimal. These results provide theoretical foundations for their practical use in analyzing sequencing data with high error rate while also providing insights for the hardness of designing ungapped LSH functions.