Central algorithms for accurately predicting non classical non-linear waves in Dense Gases over simple geometries

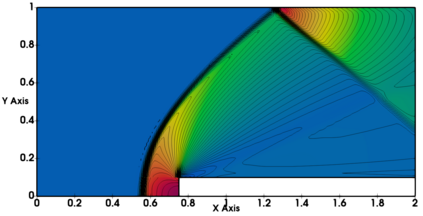
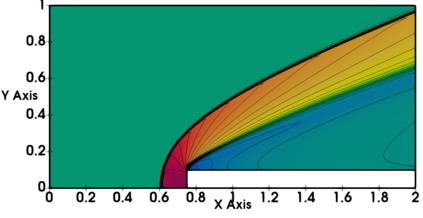
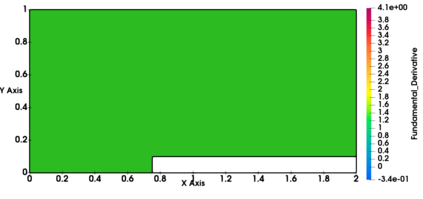
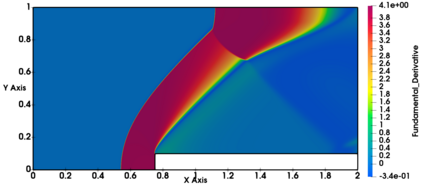
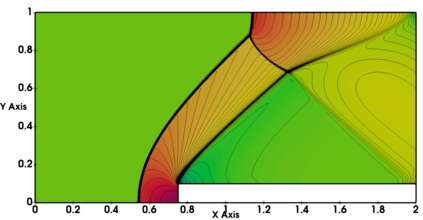
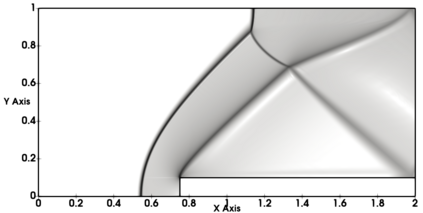
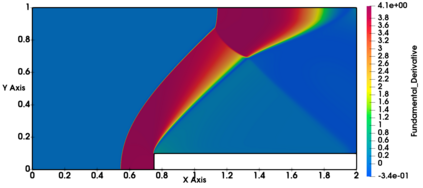
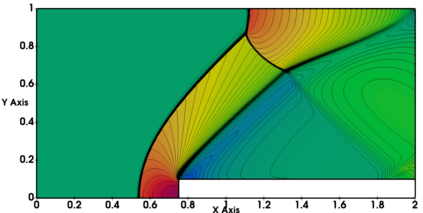
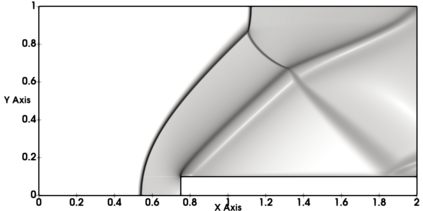
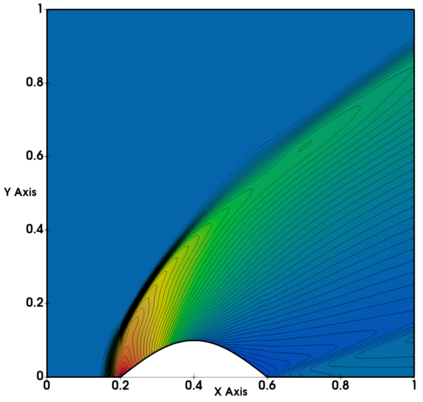
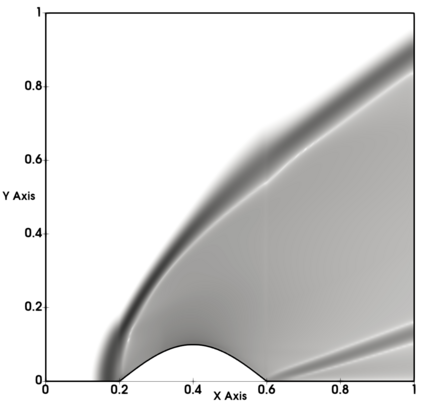
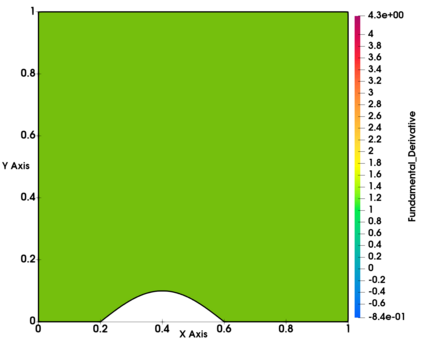
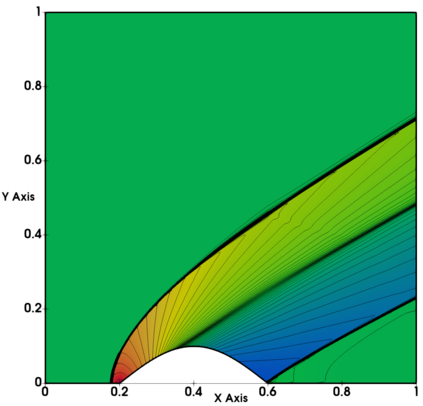
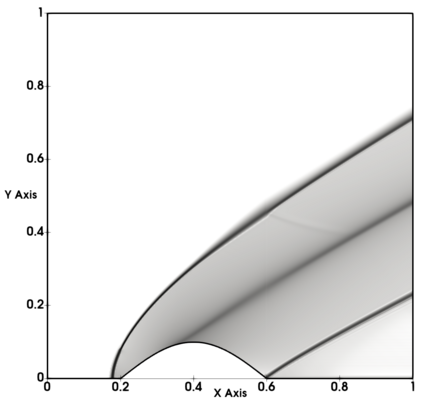
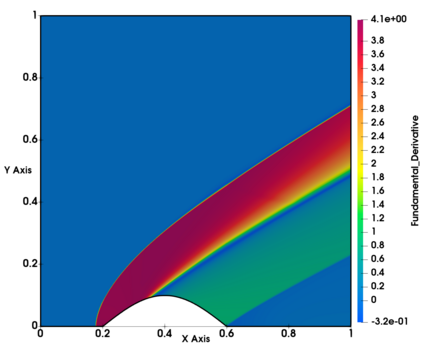
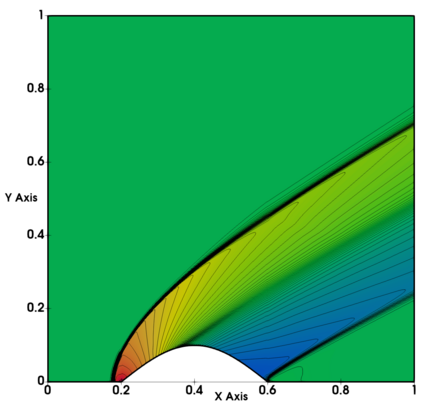
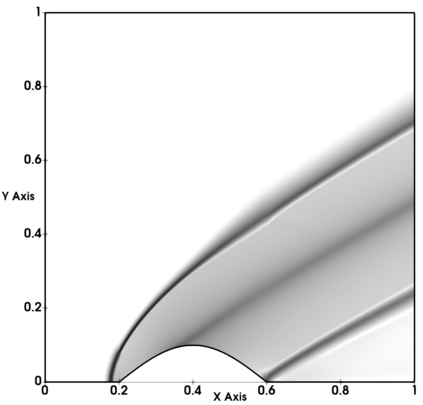
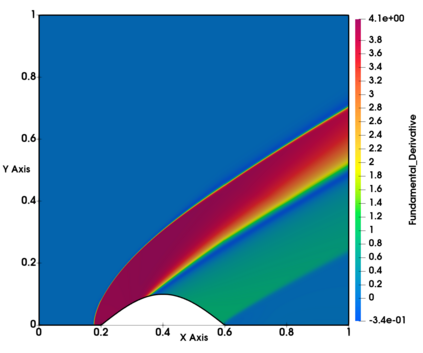
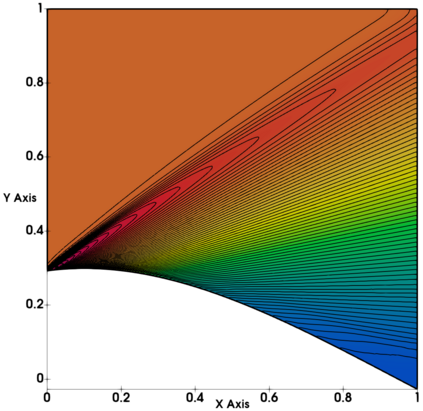
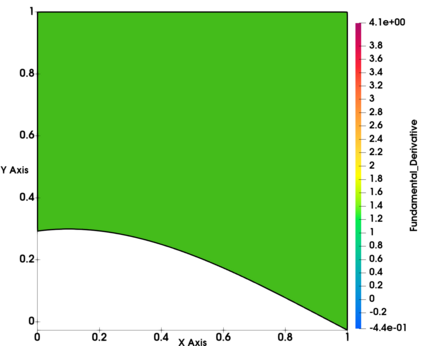
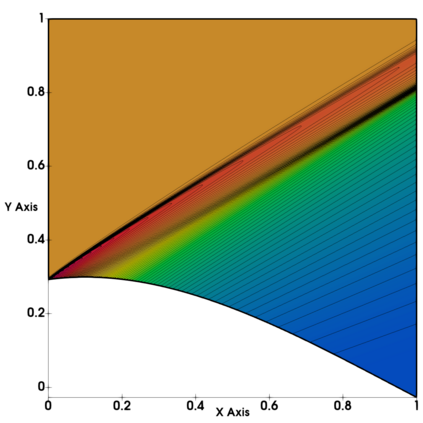
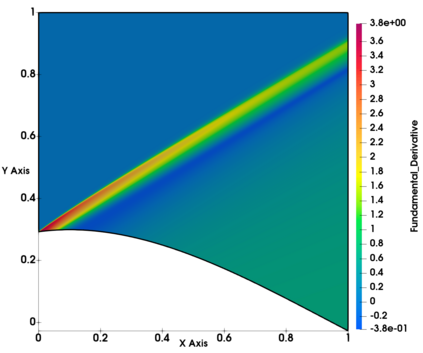
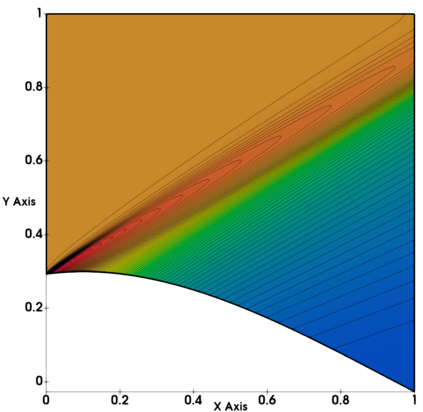
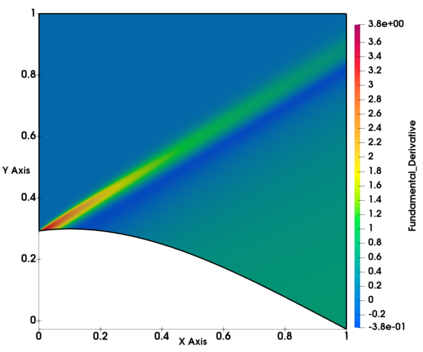
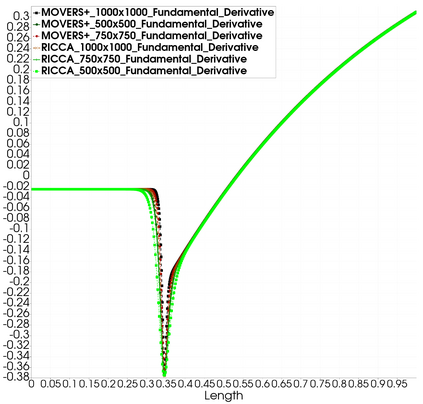
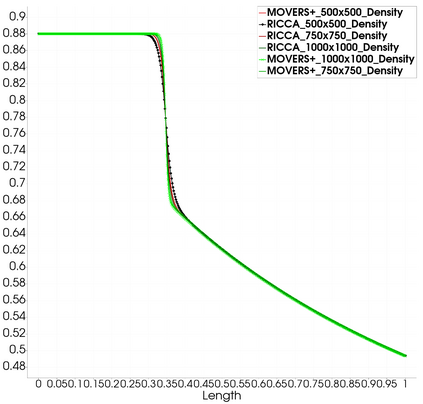
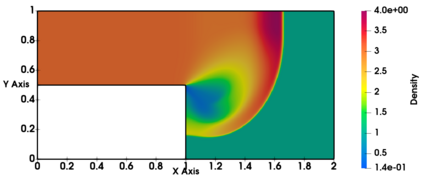
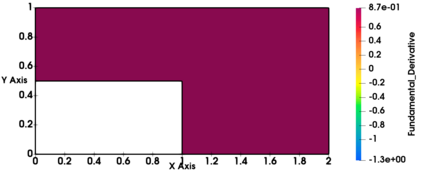
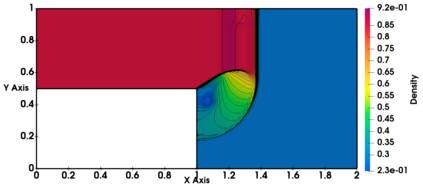
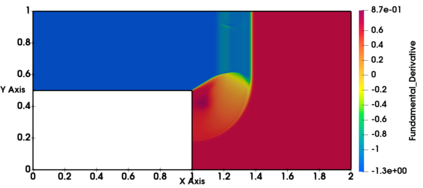
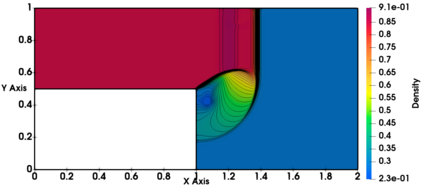
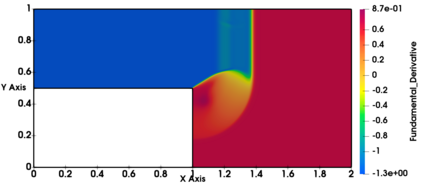
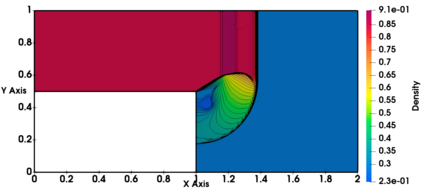
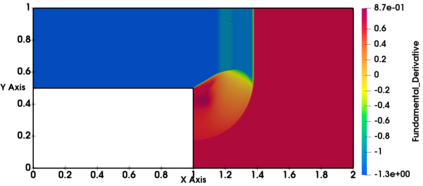
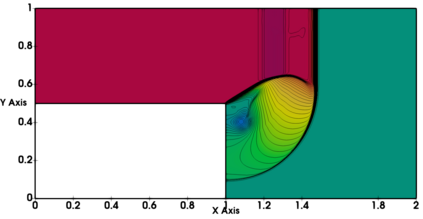
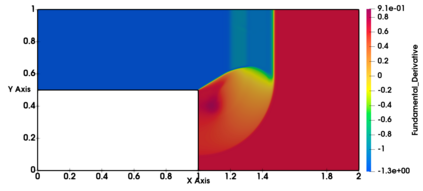
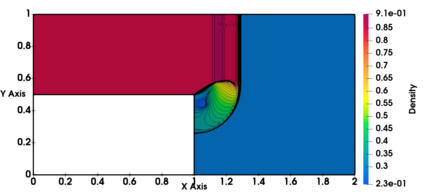
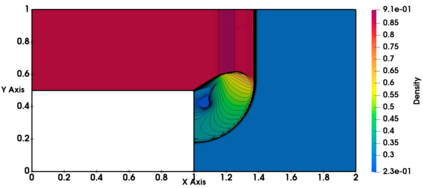
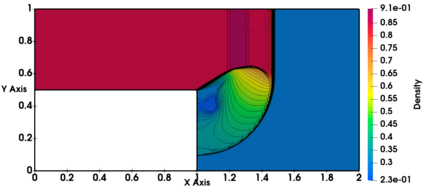
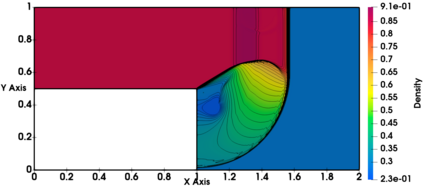
Non-classical non-linear waves exist in dense gases for large specific heats at pressures and temperatures of the order of critical point values. These waves behave precisely opposite to the classical non-linear waves, with inverted classical waves like the expansion shocks which do not violate entropy conditions. More complex equation of state (EOS) other than the ideal or perfect EOS is typically used in describing dense gases. Algorithm development with non-ideal/real gas EOS and application to dense gasses is gaining importance from a numerical perspective. Extending the algorithms designed for perfect gas EOS to dense gas flows with arbitrary real gas EOS is non-trivial. Most of the algorithms designed for prefect gas EOS are modified significantly when applied to real gas EOS. These algorithms can become complicated and some times impossible based on the EOS under consideration. The objective of the present work is to develop central solvers with smart diffusion capabilities independent of the eigenstructure and extendable to any arbitrary EOS. Euler equations with van der Waals EOS along with two newly developed algorithms, Method of Optimal Viscosity for Enhanced resolution of shocks (MOVERS+) and Riemann Invariants based Contact capturing Algorithm (RICCA), are used to simulate dense gasses over simple geometries. Various One Dimensional (1D) and Two Dimensional (2D) benchmark test cases are validated using these algorithms, and the results are compared with the those obtained from the literature.