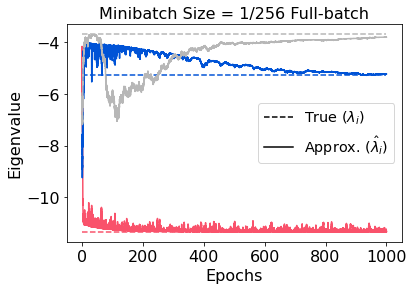
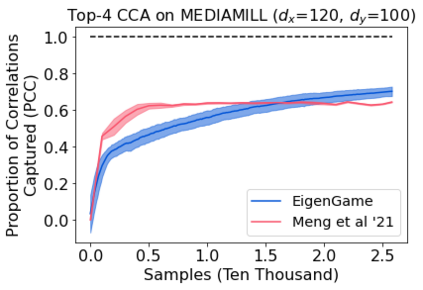
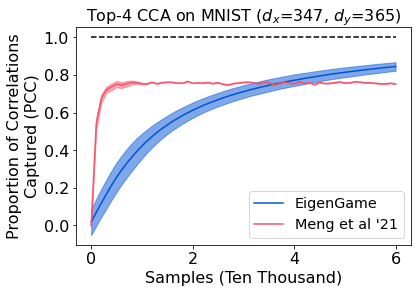
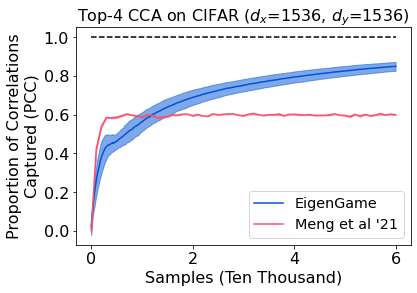
The generalized eigenvalue problem (GEP) is a fundamental concept in numerical linear algebra. It captures the solution of many classical machine learning problems such as canonical correlation analysis, independent components analysis, partial least squares, linear discriminant analysis, principal components, successor features and others. Despite this, most general solvers are prohibitively expensive when dealing with massive data sets and research has instead concentrated on finding efficient solutions to specific problem instances. In this work, we develop a game-theoretic formulation of the top-$k$ GEP whose Nash equilibrium is the set of generalized eigenvectors. We also present a parallelizable algorithm with guaranteed asymptotic convergence to the Nash. Current state-of-the-art methods require $\mathcal{O}(d^2k)$ complexity per iteration which is prohibitively expensive when the number of dimensions ($d$) is large. We show how to achieve $\mathcal{O}(dk)$ complexity, scaling to datasets $100\times$ larger than those evaluated by prior methods. Empirically we demonstrate that our algorithm is able to solve a variety of GEP problem instances including a large-scale analysis of neural network activations.
翻译:通用电子元值问题(GEP)是数字线性代数中的基本概念。 它包含许多古典机器学习问题的解决方案, 如康尼相关分析、独立部件分析、部分最小正方、线性对立分析、主要部件、后续特征等。 尽管如此, 大部分普通求解者在处理大规模数据集时费用太高, 研究却集中于寻找解决具体问题的高效方法。 在这项工作中, 我们开发了一个顶价- $k$ GEP的游戏理论配方, 其纳什平衡是通用电子元的组合。 我们还提出了一个平行的算法, 保证与纳什的无症状趋同。 目前, 最先进的方法需要 $\ mathcal{O}( d% 2k) 的复杂度, 当维度( $d$) 很大时, 其复杂性太高了。 我们展示了如何实现 $mathcal{O} (dk) 复杂度, 缩放到比先前评估的要大100\ times $100\ times than the than the lagimal lagalal assal ex ex lagal ex