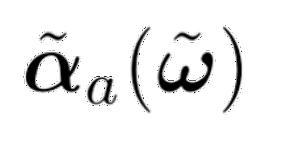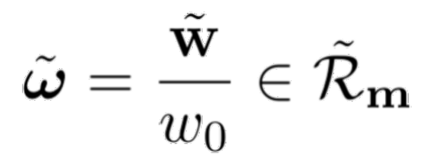We present a data-driven approach to construct entropy-based closures for the moment system from kinetic equations. The proposed closure learns the entropy function by fitting the map between the moments and the entropy of the moment system, and thus does not depend on the space-time discretization of the moment system and specific problem configurations such as initial and boundary conditions. With convex and $C^2$ approximations, this data-driven closure inherits several structural properties from entropy-based closures, such as entropy dissipation, hyperbolicity, and H-Theorem. We construct convex approximations to the Maxwell-Boltzmann entropy using convex splines and neural networks, test them on the plane source benchmark problem for linear transport in slab geometry, and compare the results to the standard, optimization-based M$_N$ closures. Numerical results indicate that these data-driven closures provide accurate solutions in much less computation time than the M$_N$ closures.
翻译:我们提出了一个数据驱动的方法,用动能方程式为瞬时系统构建基于酶的封闭装置。提议的封闭装置通过将瞬时和瞬时系统的酶之间的映射相匹配,学习了酶功能,因此不取决于瞬时系统的空间时间分解和诸如初始和边界条件等特定问题配置。有了 convex 和 $C$2 近似值,这种数据驱动封闭装置继承了基于酶封闭装置的若干结构属性,如信消散、超偏执和H-Theorem。我们利用 convex 样条和神经网络为Maxwell-Boltzmann entropy建造了螺旋近似值,在平面源基准问题上测试了它们,并将结果与标准、基于优化的M$_N$的关闭进行比较。数字结果显示,这些以数据驱动封闭装置提供的精确解决方案在计算时间比M$$的关闭时间要少得多。