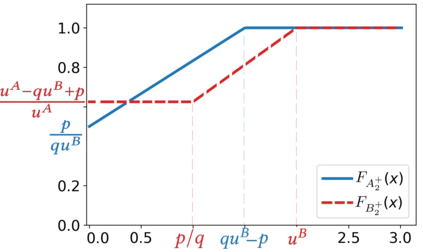
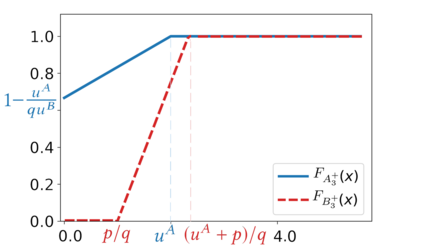
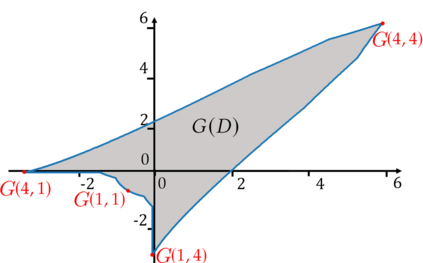
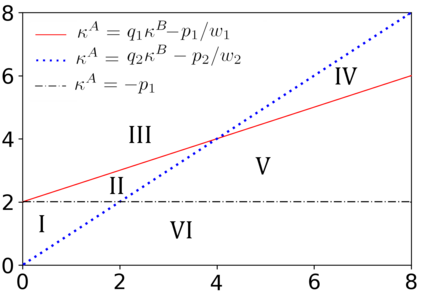
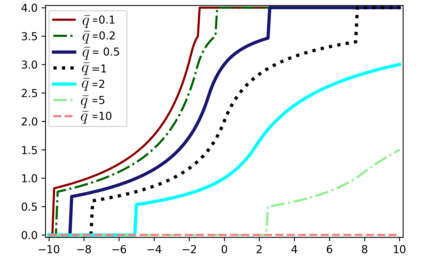
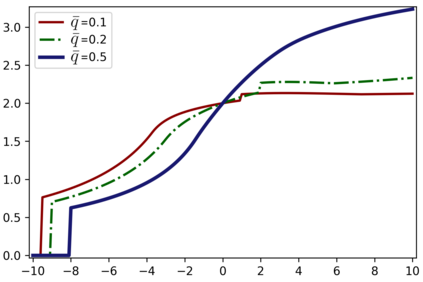
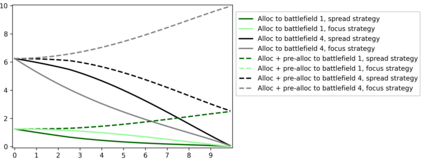
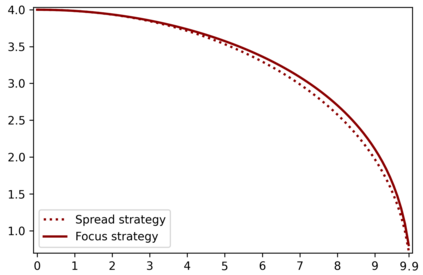
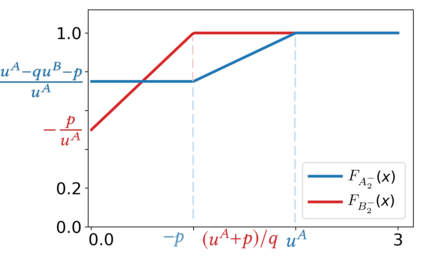
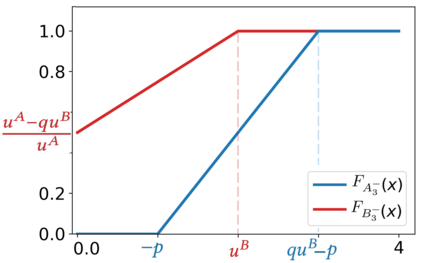
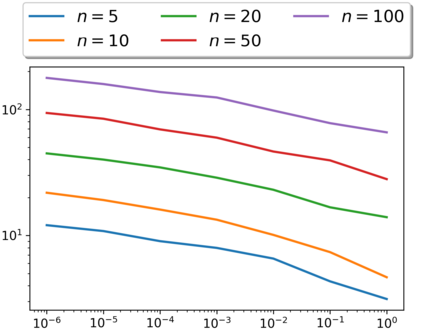
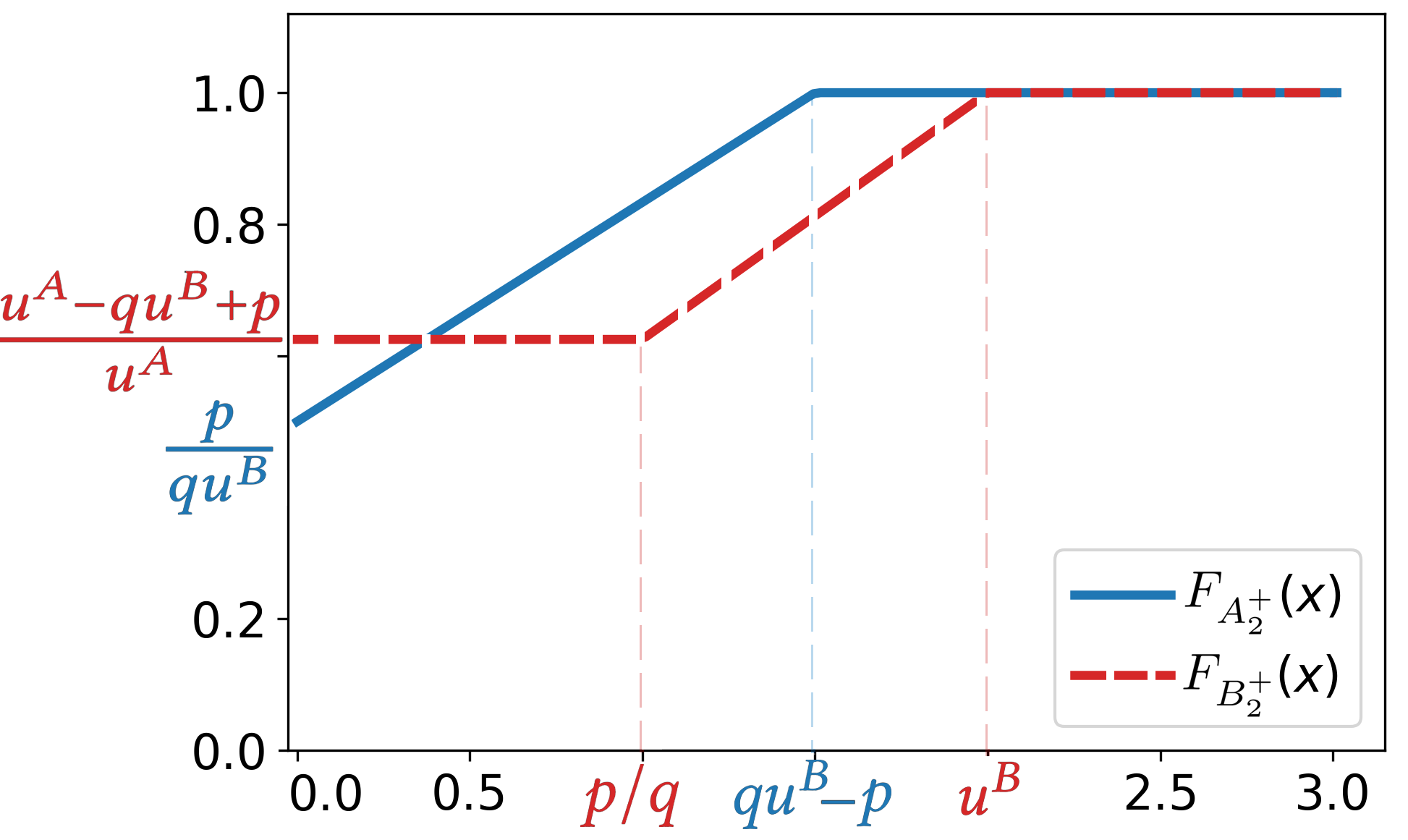
We introduce the Colonel Blotto game with favoritism, an extension of the famous Colonel Blotto game where the winner-determination rule is generalized to include pre-allocations and asymmetry of the players' resources effectiveness on each battlefield. Such favoritism is found in many classical applications of the Colonel Blotto game. We focus on the Nash equilibrium. First, we consider the closely related model of all-pay auctions with favoritism and completely characterize its equilibrium. Based on this result, we prove the existence of a set of optimal univariate distributions -- which serve as candidate marginals for an equilibrium -- of the Colonel Blotto game with favoritism and show an explicit construction thereof. In several particular cases, this directly leads to an equilibrium of the Colonel Blotto game with favoritism. In other cases, we use these optimal univariate distributions to derive an approximate equilibrium with well-controlled approximation error. Finally, we propose an algorithm -- based on the notion of winding number in parametric curves -- to efficiently compute an approximation of the proposed optimal univariate distributions with arbitrarily small error.
翻译:我们引入了以偏向为主的Blotto上校游戏,这是著名的Blotto上校游戏的延伸,在这个游戏中,获胜者自决规则被普遍化,包括每个战场上球员资源效率的预分配和不对称。这种偏向性存在于Blotto上校游戏的许多经典应用中。我们侧重于纳什均衡。首先,我们用偏向性来考虑与全薪拍卖密切相关的模型,并完全描述其平衡。根据这一结果,我们证明存在一套最佳的单向分配 -- -- 作为对平衡的候选边缘 -- -- 布洛托上校游戏的偏向性,并展示其明确的构造。在几个特定案例中,这直接导致布洛托上校游戏与偏向性之间的平衡。在另一些案例中,我们使用这些最佳的单向分配方法,以精密的近似误差来得出大致的平衡。最后,我们根据对准曲线的刮线数概念,提出了一种算法 -- -- 以便有效地对拟议的最佳的单向偏差分布进行精确的近似。