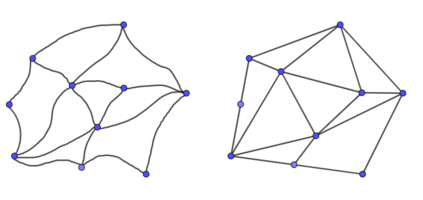
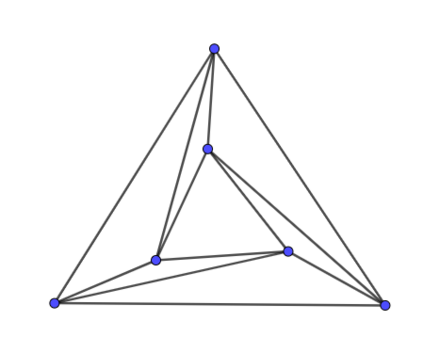
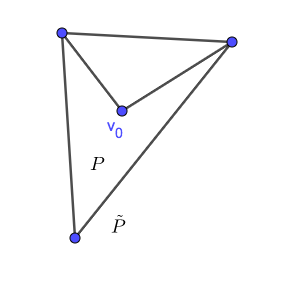
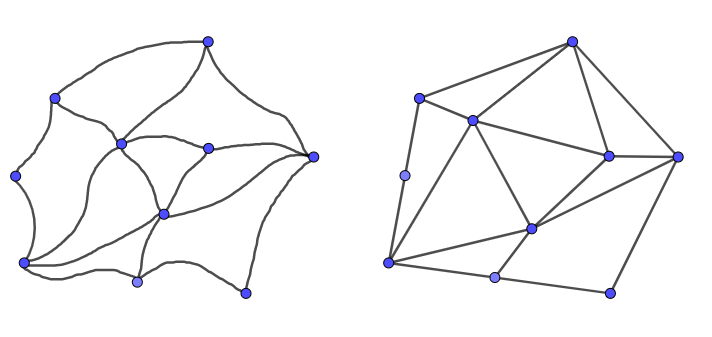
In this note, we propose a straightforward method to produce an straight-line embedding of a planar graph where one face of a graph is fixed in the plane as a star-shaped polygon. It is based on minimizing discrete Dirichlet energies, following the idea of Tutte's embedding theorem. We will call it a geodesic triangulation of the star-shaped polygon. Moreover, we study the homotopy property of spaces of all straight-line embeddings. We give a simple argument to show that this space is contractible if the boundary is a non-convex quadrilateral. We conjecture that the same statement holds for general star-shaped polygons.
翻译:在本说明中, 我们提出一个直线嵌入平面图的直线嵌入方法, 该图的一面在平面上固定为恒星形多边形。 其基础是尽量减少离散的 Dirichlet 能量, 遵循 Tutte 嵌入定理器的想法 。 我们将称之为恒星形多边形的大地三角。 此外, 我们研究所有直线嵌入空间的同质属性 。 我们给出一个简单的论点, 以显示如果边界是非星形四边形的, 则此空间是可缩合的 。 我们推测同一语句将保留为普通恒星形多边形 。