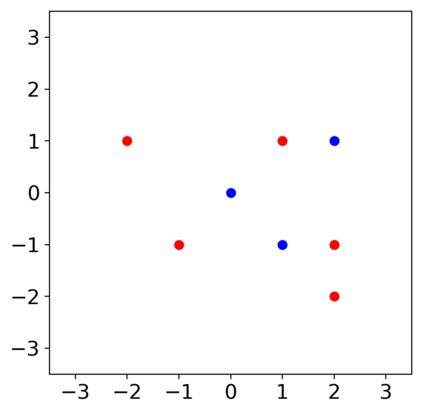
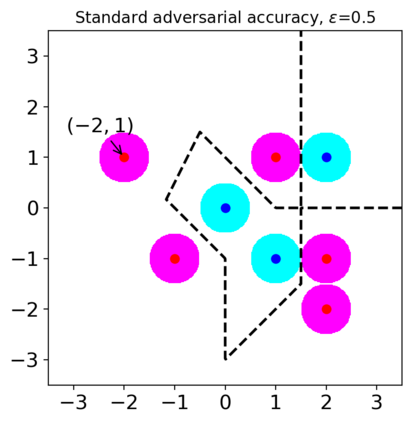
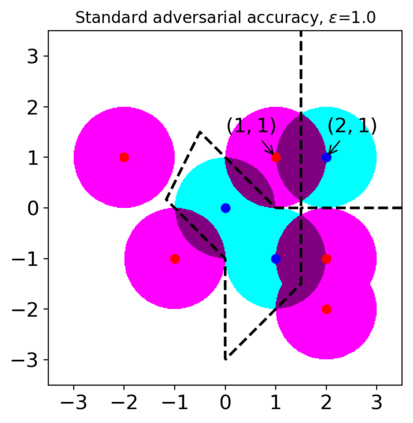
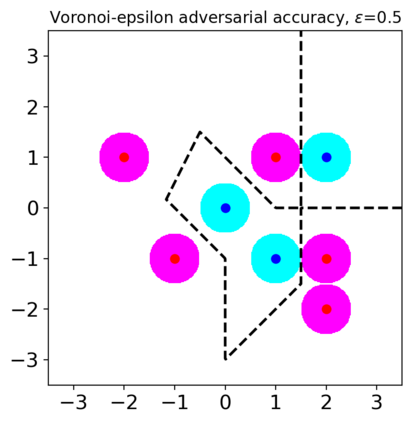
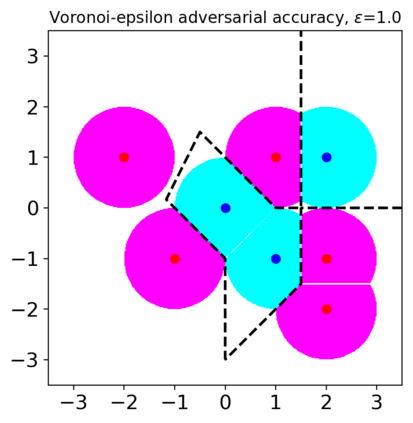
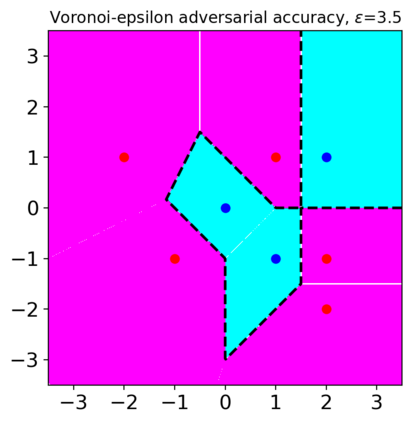
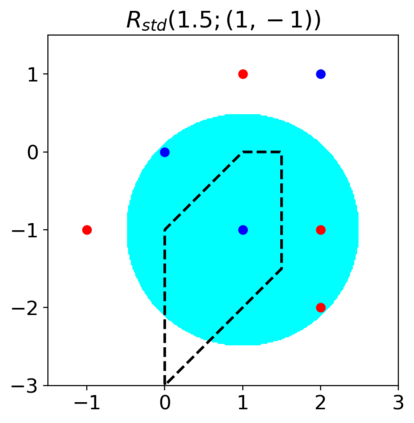
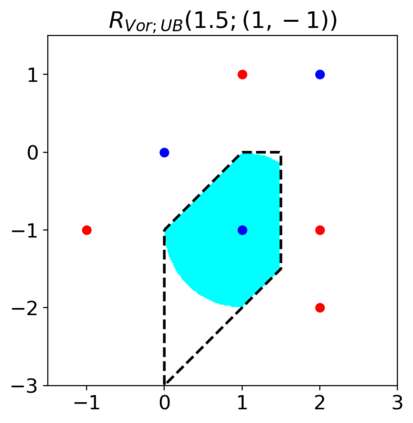
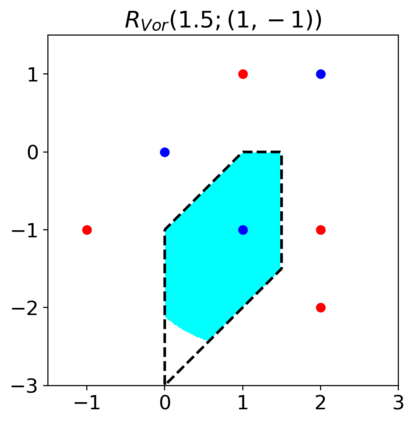
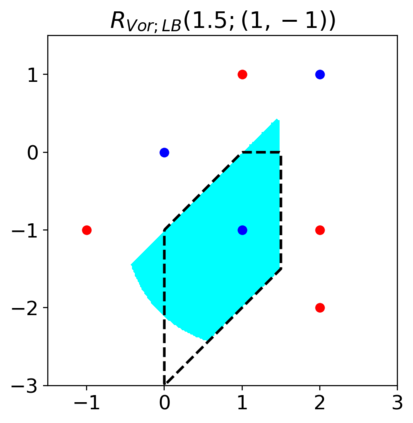
Previous studies on robustness have argued that there is a tradeoff between accuracy and adversarial accuracy. The tradeoff can be inevitable even when we neglect generalization. We argue that the tradeoff is inherent to the commonly used definition of adversarial accuracy, which uses an adversary that can construct adversarial points constrained by $\epsilon$-balls around data points. As $\epsilon$ gets large, the adversary may use real data points from other classes as adversarial examples. We propose a Voronoi-epsilon adversary which is constrained both by Voronoi cells and by $\epsilon$-balls. This adversary balances between two notions of perturbation. As a result, adversarial accuracy based on this adversary avoids a tradeoff between accuracy and adversarial accuracy on training data even when $\epsilon$ is large. Finally, we show that a nearest neighbor classifier is the maximally robust classifier against the proposed adversary on the training data.
翻译:以往关于稳健性的研究认为,准确性和对抗性准确性之间是权衡的。即使我们忽略了一般化,这种权衡也是不可避免的。我们争辩说,这种权衡性是常用的对抗性准确性定义所固有的。 对抗性准确性定义使用一个对手,可以在数据点周围构建受美元-美元-球制约的对立点。随着美元数额的提高,对手可以使用其他类别的真实数据点作为抗辩性例子。我们提议了Voronio-epsilon对立的Voronioi-epsilon对立,但受到Voronoi细胞和美元-球的制约。这种对立性对立性平衡是两种对立概念之间的平衡。因此,基于这一对手的对抗性准确性避免了培训数据在准确性和对抗性对立性精确性之间的权衡,即使$-美元数额很大。最后,我们表明,最近的邻居分类是针对拟议培训数据对手的最有力的分类。