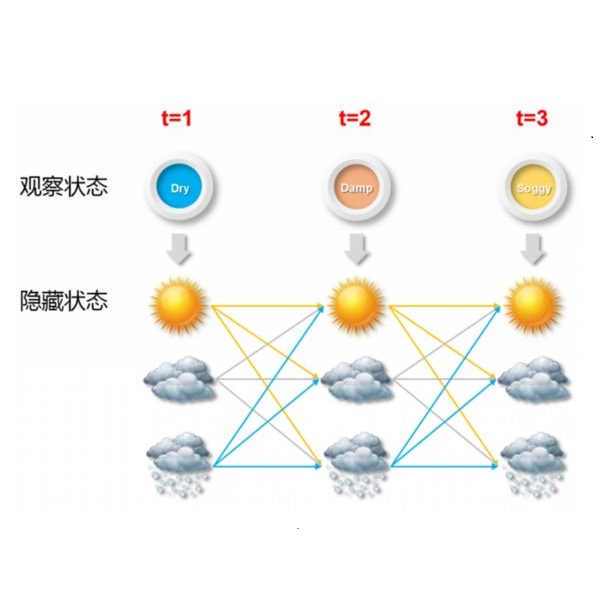
Environmental time series data observed at high frequencies can be studied with approaches such as hidden Markov and semi-Markov models (HMM and HSMM). HSMMs extend the HMM by explicitly modeling the time spent in each state. In a discrete-time HSMM, the duration in each state can be modeled with a zero-truncated Poisson distribution, where the duration parameter may be state-specific but constant in time. We extend the HSMM by allowing the state-specific duration parameters to vary in time and model them as a function of known covariates observed over a period of time leading up to a state transition. In addition, we propose a data subsampling approach given that high-frequency data can violate the conditional independence assumption of the HSMM. We apply the model to high-frequency data collected by an instrumented buoy in Lake Mendota. We model the phycocyanin concentration, which is used in aquatic systems to estimate the relative abundance of blue-green algae, and identify important time-varying effects associated with the duration in each state.
翻译:在高频观测的环境时间序列数据可以使用隐藏的Markov和半Markov模型(HMM和HSMM)等方法进行研究。 HSMMs通过对每个州的时间进行明确模拟来延长HMMM。在一个离散的HSMM中,每个州的时间长度都可以用零流波森分布模型来模拟,其持续时间参数可以是特定状态,但时间是恒定的。我们延长HSMMM,允许特定州的时间参数在时间上有所变化,并将这些参数作为在一段期间观察到的已知共变系数的函数来模拟,直至国家转型。此外,我们建议一种数据分样方法,因为高频数据可能违反HSMMM的有条件独立假设。我们将该模型应用于在门多托塔湖仪器浮标定的高频数据。我们模拟了在水生系统中用来估计蓝绿色藻相对丰度的植物浓度,并查明与每个州持续时间相关的重要时间变化效应。