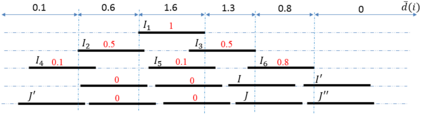
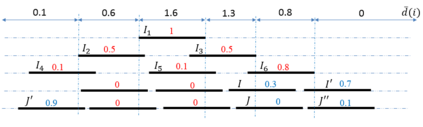
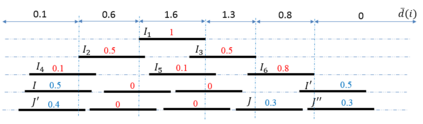
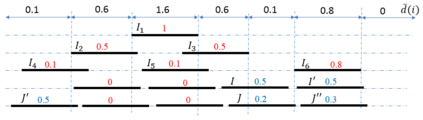
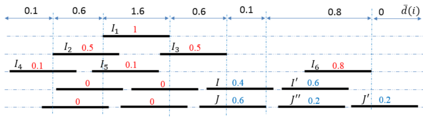
In the rectangle stabbing problem, we are given a set $\cR$ of axis-aligned rectangles in $\RR^2$, and the objective is to find a minimum-cardinality set of horizontal and/or vertical lines such that each rectangle is intersected by one of these lines. The standard LP relaxation for this problem is known to have an integrality gap of 2, while a better intergality gap of 1.58.. is known for the special case when $\cR$ is a set of horizontal segments. In this paper, we consider two more special cases: when $\cR$ is a set of horizontal and vertical segments, and when $\cR$ is a set of unit squares. We show that the integrality gap of the standard LP relaxation in both cases is stricly less than $2$. Our rounding technique is based on a generalization of the {\it threshold rounding} idea used by Kovaleva and Spieksma (SIAM J. Disc. Math 2006), which may prove useful for rounding the LP relaxations of other geometric covering problems.
翻译:在矩形刺刺问题中,我们得到了一套固定轴对齐矩形的固定矩形的值$/CR$2美元,目标是找到一套水平和/或垂直的最小心性线,使每个矩形被其中一条线交叉。众所周知,这个问题的标准LP松绑是2个整体性差,而1.58是更好的星际差。当$\CR$是一组水平段时,就是一个特例。在本文中,我们考虑两个更特殊的情况:当$\CR$是一组水平和垂直区块时,当$\CR$是一组单位方块时,当$\CR$是一组单位方块时。我们表明,两种情况下标准的LP松绑的一体化差距都小于2美元。我们的圆形技术基于Kovaleva和Spieksma(SIM J. Disc. Math (2006) ) 所使用的 立点点概念的概括化,这可能会被证明有助于四舍LP对其他几度问题的宽。