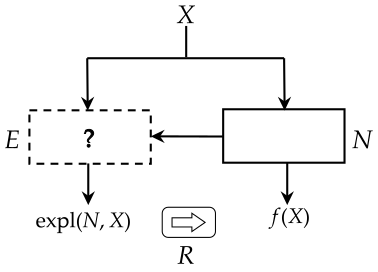
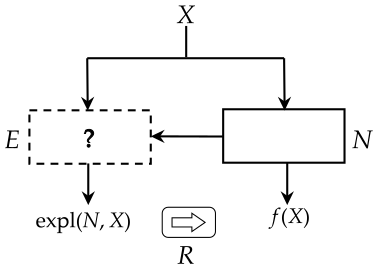
Explainable components in XAI algorithms often come from a familiar set of models, such as linear models or decision trees. We formulate an approach where the type of explanation produced is guided by a specification. Specifications are elicited from the user, possibly using interaction with the user and contributions from other areas. Areas where a specification could be obtained include forensic, medical, and scientific applications. Providing a menu of possible types of specifications in an area is an exploratory knowledge representation and reasoning task for the algorithm designer, aiming at understanding the possibilities and limitations of efficiently computable modes of explanations. Two examples are discussed: explanations for Bayesian networks using the theory of argumentation, and explanations for graph neural networks. The latter case illustrates the possibility of having a representation formalism available to the user for specifying the type of explanation requested, for example, a chemical query language for classifying molecules. The approach is motivated by a theory of explanation in the philosophy of science, and it is related to current questions in the philosophy of science on the role of machine learning.
翻译:XAI 算法中可解释的组成部分往往来自一套熟悉的模型,如线性模型或决策树。我们制定了一种方法,根据规格指导所制作的解释类型;从用户那里了解规格,可能利用与用户的相互作用和来自其他领域的贡献;可以取得规格的领域包括法医学、医学和科学应用;在某一领域提供可能的规格类型的菜单是算法设计者的探索性知识表述和推理任务,目的是了解高效可比较的解释模式的可能性和局限性。我们讨论了两个例子:用理论解释巴伊西亚网络的解释,以及图形神经网络的解释。后一案例说明了用户可以使用一种代表形式来说明所要求的解释类型的可能性,例如用于对分子进行分类的化学查询语言。这一方法的动机是科学哲学解释理论的理论,它与目前科学哲学中关于机器学习作用的问题有关。