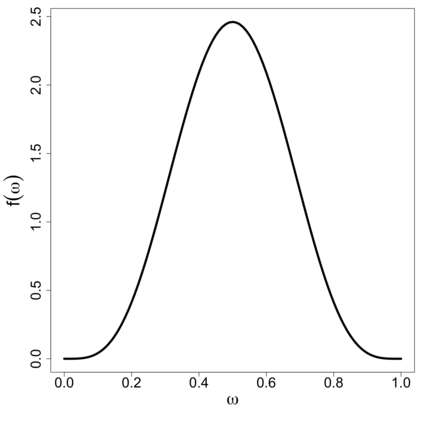
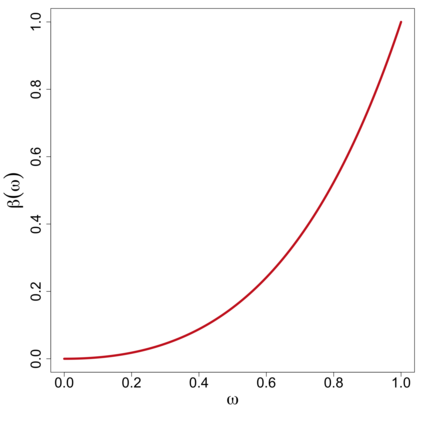
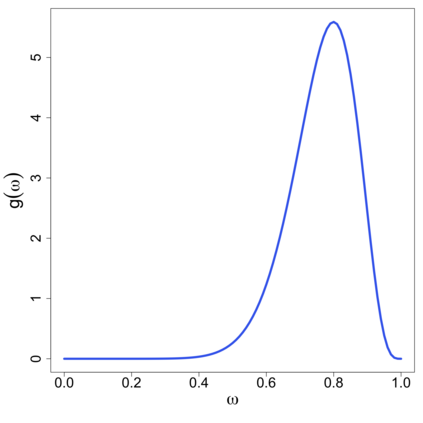
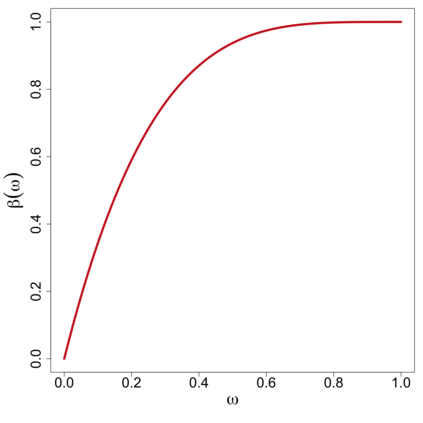
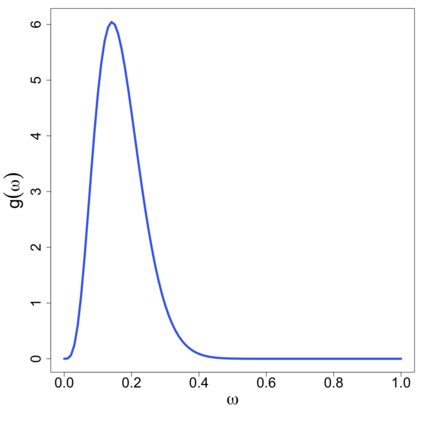
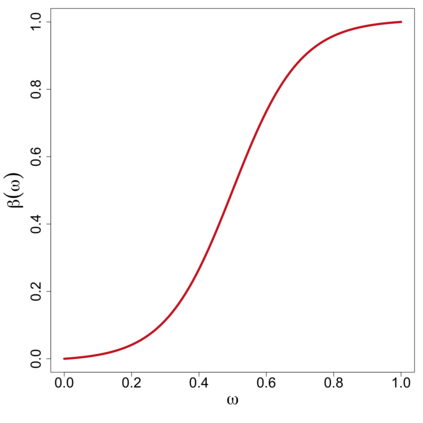
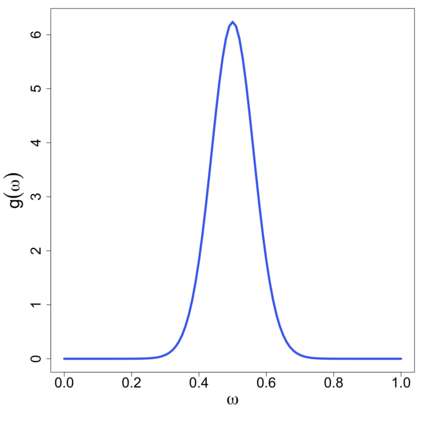
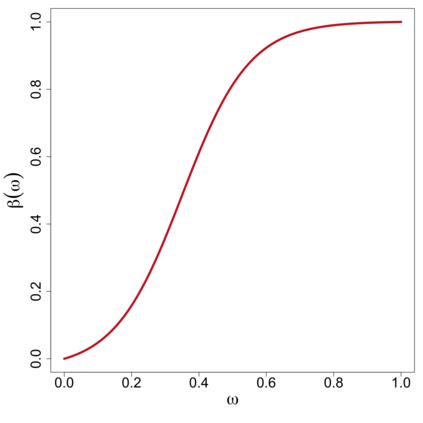
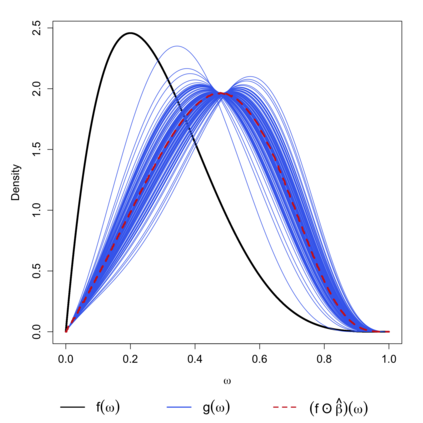
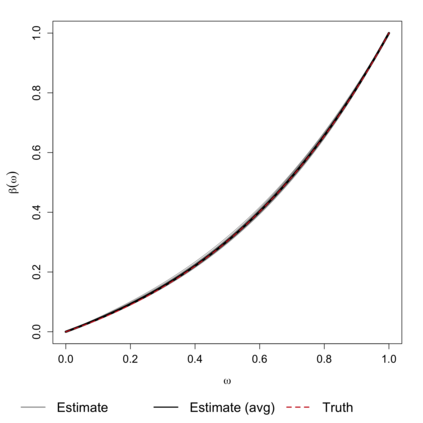
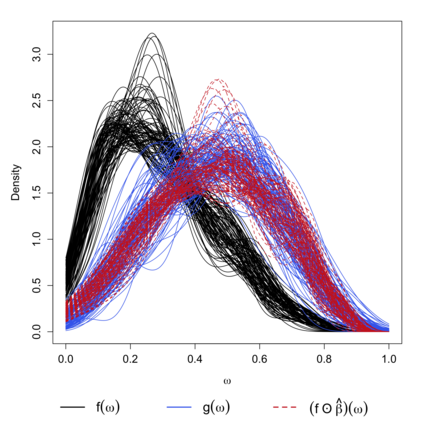
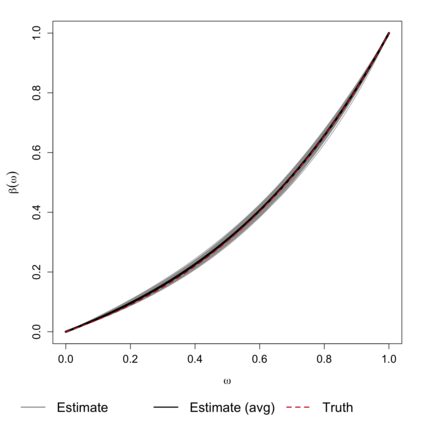
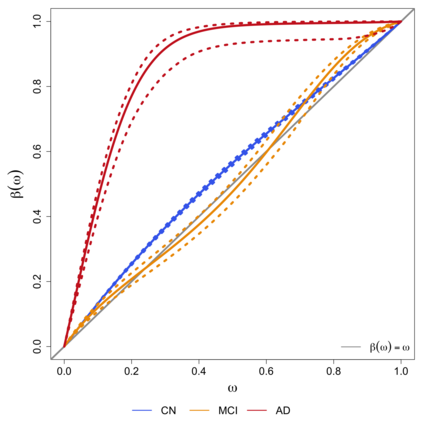
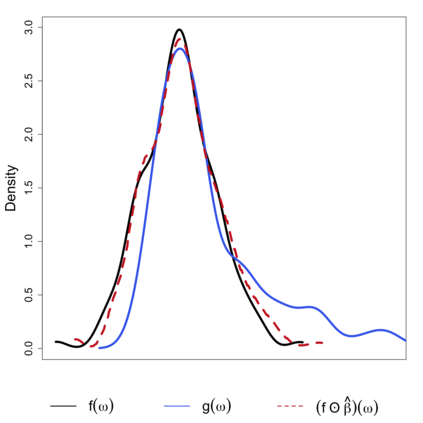
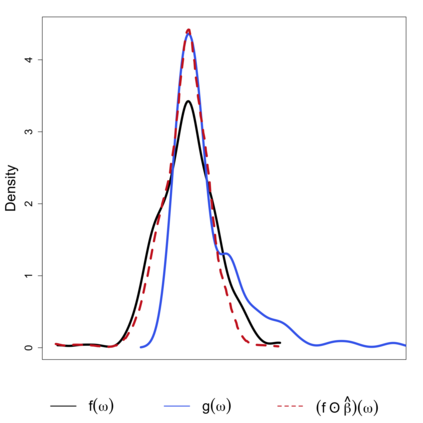
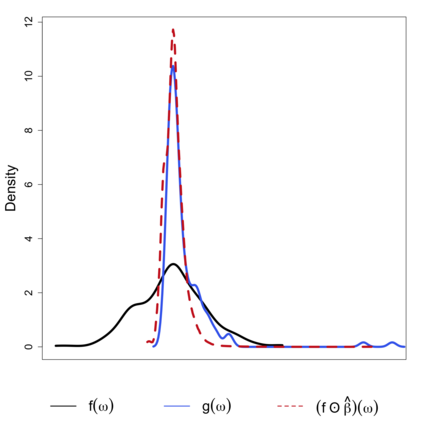
In this study, a density-on-density regression model is introduced, where the association between densities is elucidated via a warping function. The proposed model has the advantage of a being straightforward demonstration of how one density transforms into another. Using the Riemannian representation of density functions, which is the square-root function (or half density), the model is defined in the correspondingly constructed Riemannian manifold. To estimate the warping function, it is proposed to minimize the average Hellinger distance, which is equivalent to minimizing the average Fisher-Rao distance between densities. An optimization algorithm is introduced by estimating the smooth monotone transformation of the warping function. Asymptotic properties of the proposed estimator are discussed. Simulation studies demonstrate the superior performance of the proposed approach over competing approaches in predicting outcome density functions. Applying to a proteomic-imaging study from the Alzheimer's Disease Neuroimaging Initiative, the proposed approach illustrates the connection between the distribution of protein abundance in the cerebrospinal fluid and the distribution of brain regional volume. Discrepancies among cognitive normal subjects, patients with mild cognitive impairment, and Alzheimer's disease (AD) are identified and the findings are in line with existing knowledge about AD.
翻译:暂无翻译