Proper decision trees: An axiomatic framework for solving optimal decision tree problems with arbitrary splitting rules

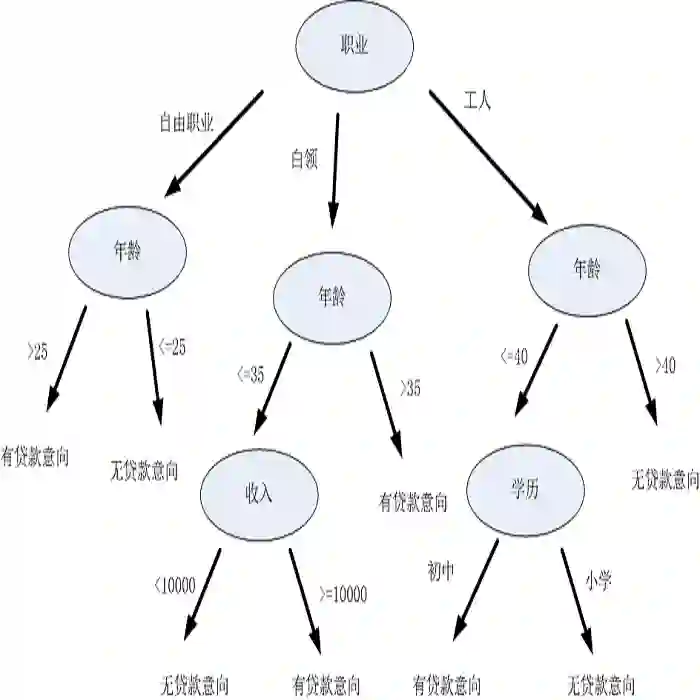
We present an axiomatic framework for analyzing the algorithmic properties of decision trees. This framework supports the classification of decision tree problems through structural and ancestral constraints within a rigorous mathematical foundation. The central focus of this paper is a special class of decision tree problems-which we term proper decision trees-due to their versatility and effectiveness. In terms of versatility, this class subsumes several well-known data structures, including binary space partitioning trees, K-D trees, and machine learning decision tree models. Regarding effectiveness, we prove that only proper decision trees can be uniquely characterized as K-permutations, whereas typical non-proper decision trees correspond to binary-labeled decision trees with substantially greater complexity. Using this formal characterization, we develop a generic algorithmic approach for solving optimal decision tree problems over arbitrary splitting rules and objective functions for proper decision trees. We constructively derive a generic dynamic programming recursion for solving these problems exactly. However, we show that memoization is generally impractical in terms of space complexity, as both datasets and subtrees must be stored. This result contradicts claims in the literature that suggest a trade-off between memoizing datasets and subtrees. Our framework further accommodates constraints such as tree depth and leaf size, and can be accelerated using techniques such as thinning. Finally, we extend our analysis to several non-proper decision trees, including the commonly studied decision tree over binary feature data, the binary search tree, and the tree structure arising in the matrix chain multiplication problem. We demonstrate how these problems can be solved by appropriately modifying or discarding certain axioms.