Graph coarsening: From scientific computing to machine learning

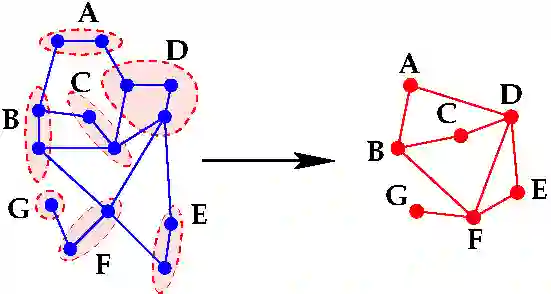
The general method of graph coarsening or graph reduction has been a remarkably useful and ubiquitous tool in scientific computing and it is now just starting to have a similar impact in machine learning. The goal of this paper is to take a broad look into coarsening techniques that have been successfully deployed in scientific computing and see how similar principles are finding their way in more recent applications related to machine learning. In scientific computing, coarsening plays a central role in algebraic multigrid methods as well as the related class of multilevel incomplete LU factorizations. In machine learning, graph coarsening goes under various names, e.g., graph downsampling or graph reduction. Its goal in most cases is to replace some original graph by one which has fewer nodes, but whose structure and characteristics are similar to those of the original graph. As will be seen, a common strategy in these methods is to rely on spectral properties to define the coarse graph.